Two subjects are compulsory for a student in an examination. In how many ways can a student select 5 subjects out of given 10 subjects?
Two subjects are compulsory.
∴ No. of ways of selecting remaining 3 subjects from the remaining 8 subjects
=.8C3
=8!3!5!=56
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - PERMUTATION AND COMBINATION EXERCISE - Exercise A9videos
PERMUTATION AND COMBINATION
- BOOK - NAGEEN PRAKASHANCHAPTER - PERMUTATION AND COMBINATION EXERCISE - Exercise B10videos
PERMUTATION AND COMBINATION
- BOOK - NAGEEN PRAKASHANCHAPTER - MATHEMATICAL REASONING EXERCISE - Misellaneous exercise7videos
MATHEMATICAL REASONING
- BOOK - NAGEEN PRAKASHANCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Exercise 429videos
PRINCIPLE OF MATHEMATICAL INDUCTION
Similar Questions
In how many ways can 4 books be selected out of 16 books on different subjects?
View SolutionIn how many ways can 4 books be selected out of 16 books on different subjects?
View SolutionIt is necessary to pass in each subject out of 7 subjects in an examination. In how many ways can a student failed?
View SolutionHow many ways 3 students can be selected from 50 students ?
View SolutionFrom a class of 40 students, in how many ways can five students be chosen
(ii) As subject monitor (one from each subject)View SolutionIn how many ways can 5 subjects be chosen from 9 subjects if three subjects are compulsory?
View SolutionIt is required to get minimum marks in each subject out of 5 subject to pass in an examination. In how many ways can a student fail?
View SolutionOut of 180 students in a class 7 students failed in all the three subjects viz. Physics, Chemistry, Maths only 144 students pass in only one subject and 21 students pass in only two subjects. How many students passed in at most two subjects but atleast in one subject?
View SolutionIn a class of 80 students, 55 students passed in mathematics and 60 passed in chemistry. 10 stu-dents failed in both mathematics and chemistry.
(i) How many students passed in both the subjects ?
(ii) How many students passed in exactly one of the two subjects ?View SolutionThe given pie chart shows the marks obtained in degrees) by a student in different subjects. The total marks obtained by the student in the examination is 432.
In how many subjects marks obtained are more than the average marks per subject?
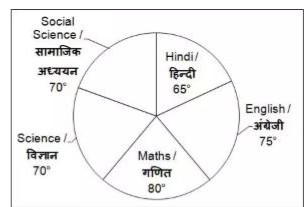 View Solution
View Solution


