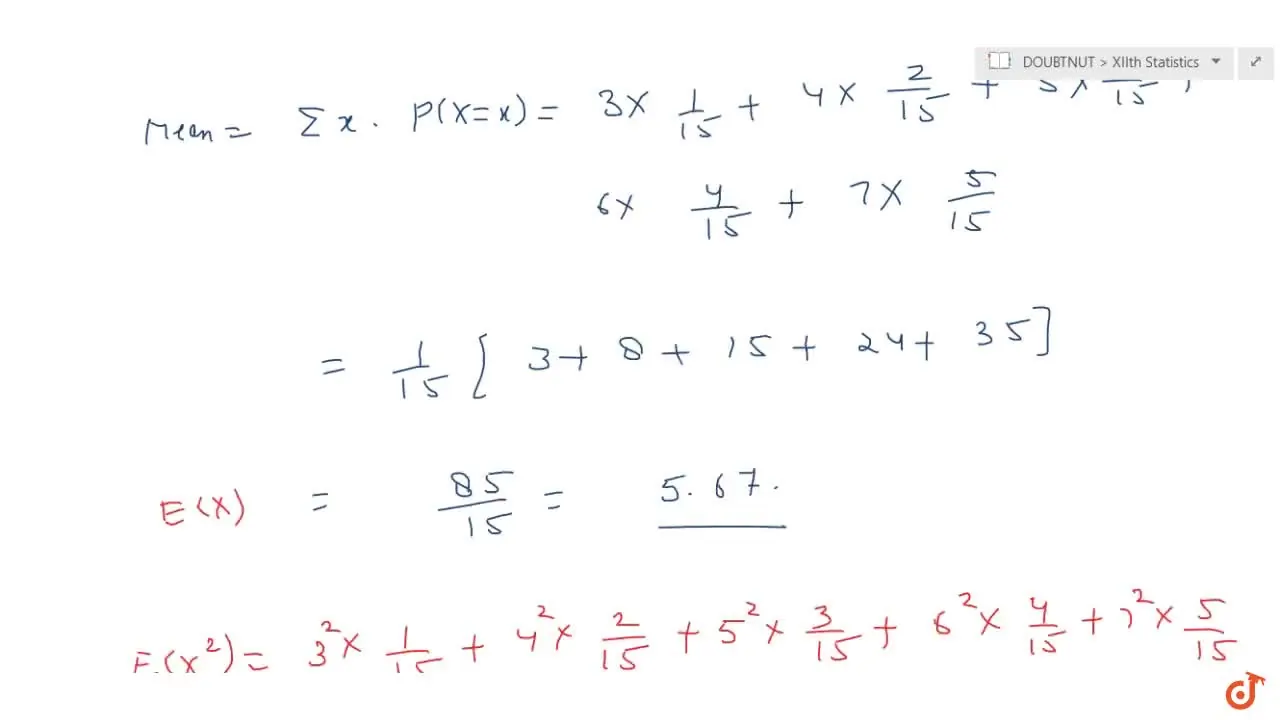Two numbers are selected are random (without replacement) from positive integers 2, 3, 4, 5, 6 and 7. Let X denote the larger of the two numbers obtained. Find the mean and variance of the probability distribution of X.
Here are some positive integers (2,3,4,5,6,7) from which two numbers are selected at random (without replacement) and from those selected numbers larger one is selected.
Smallest pair that can be formed (2,3) and Largest pair (6,7) therefore minimum value for X is 3 and maximum is 7.
P(X=3)=P{(2,3),(3,2)}=P(2,3)+P(3,2)
=16⋅15+16⋅15
P(X=3)=115
Similarly,
P(X=4)=215
P(X=5)=15
P(X=6)=415
P(X=7)=13
Mean=Σx.P(X=x)=3⋅115+4⋅215+5⋅315+6⋅415+7⋅515
=115[3+8+15+24+35]
=8515=5.67
E(x2)=32⋅115+42⋅215+52⋅315+14415+24515
=115[9+32+75+144+245]
=33.67
Therefore, Variance (x)=E(E2)−E(X)2
=33.67−(5.67)2
=1.52
Related Playlists
Similar Questions
Two numbers are selected at random (without replacement) from positive integers 2,3,4,5,6, and 7 . Let X denote the larger of the two numbers obtained. Find the mean and variance of the probability distribution of X .
View SolutionTwo numbers are selected at random(without replacement) from the first five positive integers. Let X denote the larger of the two numbers obtained. Find the mean and variance of X
View SolutionTwo numbers are selected at random (without replacement) from the first six positive integers. Let X denote the larger of the two numbers obtained. Find E(X).
View SolutionTwo numbers are selected at random (without replacement) from first six positive integers. Let X denote the larger of the two numbers obtained. Find the probability distribution of X. Find the mean and variance of this distribution.
View Solutionthree numbers are selected at random (without replacement) from first six positive integers. Let X denote the largest of the three numbers obtained. the probability distribution of X. Also, find the mean
View SolutionTwo numbers are selected at random (without replacement) from first 7 natural numbers. If X denotes the smaller of the two numbers obtained, find the probability distribution of X. Also, find mean of the distribution.
View SolutionLet X denote the sum of the numbers obtained when two fair dice are rolled. Find the variance and standard deviation of X.
View SolutionTwo dice are rolled at random 5 times. Obtain the mean and variance of the distribution of doublets obtained.
View SolutionThe difference between C.I. and S.I. at a certain rate on rs. 2000 at the end of 2years is rs.12.8. The rate of inerest is:
View SolutionTwo numbers b and c are chosen at random with replacement from the numbers 1, 2, 3, 4, 5, 6, 7, 8 and 9. The probability that x2+bx+c>0forallξnR, is
View Solution