Two lines l and m interset at the O and P is Point on a line n Passing through the point O such that P is equidistant from l and m. Prove that n is the bisectof the angle formed by l and m
Given two lines l and m intersect at the point O and P is a point on a line n Passing though O such that P is equidistant from l and m i.e PQ=PR
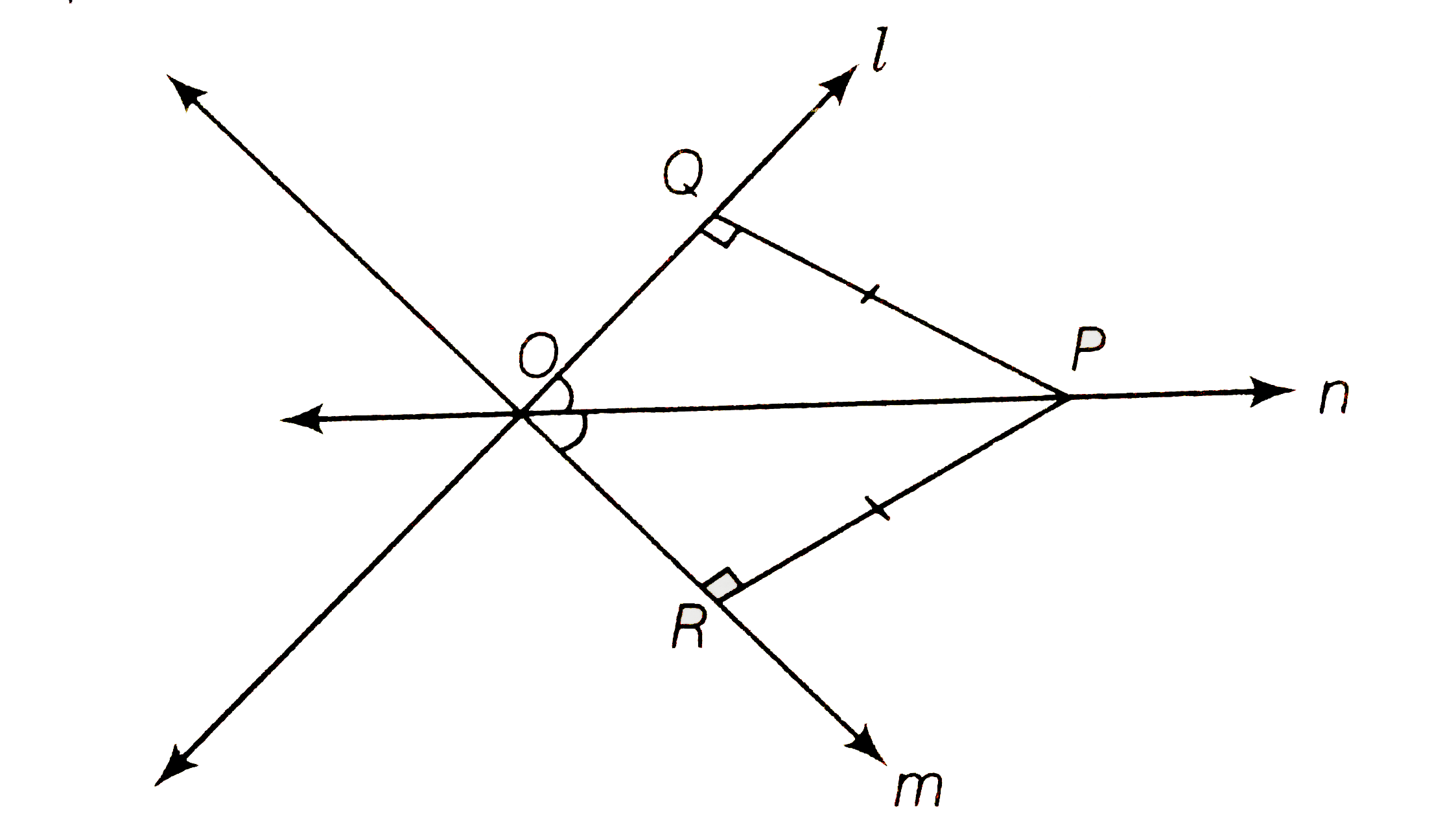
To prove n is the bisector of the angle formed by l and m i.e n is the bisector of ∠QOR.
Proof in ΔOQPandΔORP
∠PQO=∠PRO=90∘
[since P in equlidistant from l and m so PQ and PR should be Perpendicular to lines l and m repectively ]
OP =OP [Common side ]
PQ=PR [given ]
∴ΔOQP≅ΔORP [by RHS congruence rule ]
⇒∠POQ=∠POR [by CPCT]
Hence ,n is the bisector of ∠QOR
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER TYPE QUESTIONS11videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS12videos
STATISTICS AND PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VOLUME AND SURFACE AREAEXERCISE - LONG ANSWER TYPE QUESTIONS8videos
VOLUME AND SURFACE AREA
Similar Questions
AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionBM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If L is the mid-point of BC, prove that LM=LN.
View SolutionIn the given figure , obtain all the points equidistant from lines m and n, and 2.5 cm from O.
 View Solution
View SolutionP is a point equidistant from two lines l and m intersecting at a point A, Show that AP bisects the angle between them.
View SolutionBM and CN are perpendicular to a line passing through the vertex A of a triangle ABC. If L is the mid-point of BC , prove that LM=LN.
View SolutionIf P is any point on the plane lx+my+nz=pandQ is a point on the line OP such that OP.OQ=p2 , then find the locus of the point Q.
View SolutionIf P is any point on the plane lx+my+nz=pandQ is a point on the line OP such that OP.OQ=p2 , then find the locus of the point Q.
View SolutionLOL' and MOM' are two chords of parabola y2=4ax with vertex A passing through a point O on its axis. Prove that the radical axis of the circles described on LL' and MM' as diameters passes though the vertex of the parabola.
View SolutionIf l, m,n are three lines such that l∣∣m and n⊥l, prove that n⊥m.
View Solution


