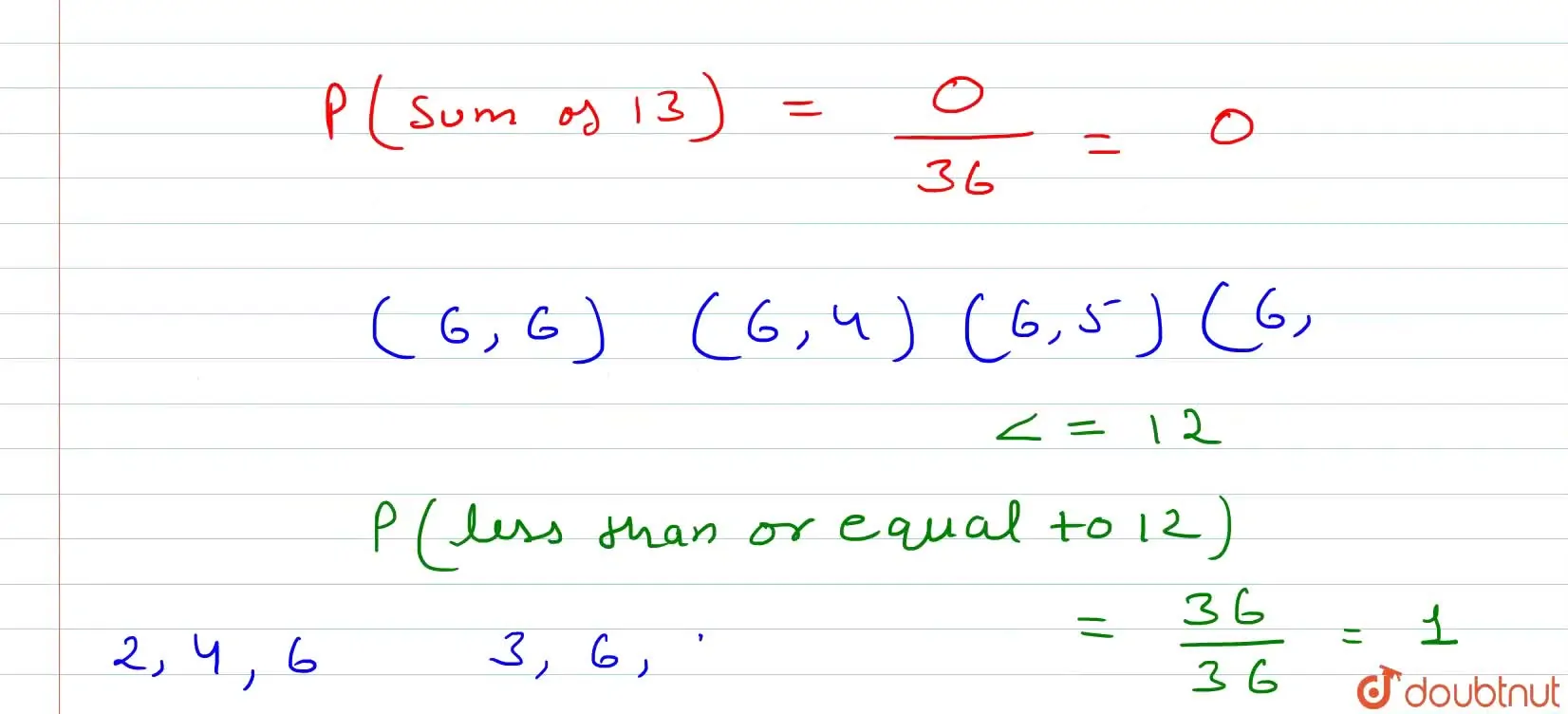Two different dice are thrown simultaneously. What is the probability that the sum of two number appearing on the top of dice is.
(i) 9 (ii) 10 (iii) at least 10 (iv) 13 (v) less than or equal 12
(vi) a multiple of 2 on one die and a multiple of 3 on the other die ?
When two different dice are thrown, the total number of outcomes is 36 and all the out-comes are equally likely.
(i) The outcomes favourable to the event 'sum of two number is 9' are (6, 3), (5, 4), (4, 5) and (3, 6) these are 4 in number.
∴ P (sum of 9) =436=19.
(ii) The outcomes favourable to the event 'sum of two numbers is 10' are (6, 4), (5, 5) and ( 4, 6). These are 3 in number.
∴ P (sum of 10) =336=112.
(iii) The sum of at least 10 mean that sum is 10, 11 or 12. Therefore, the outcomes favourable to the event 'sum of at least 10' are (6, 4), (5, 5), (4, 6), (6, 5), (5, 6) and ( 6, 6). These are 6 in number.
∴ P (sum of at least 10) =636=16.
(iv) As the sum of two number appearing on the top of two dice can never be 13, there is no outcomes favourable to the event 'sum of two numbers is 13'.
∴ P (sum of 13) =036=0.
(v) As the sum of two numbers appearing on the top of two dice is always less than or equal to 12, all the 36 outcomes are favourable to the event 'sum is less than or equal to 12'.
∴ P (sum is less than or equal to 12) =3636=1.
(vi) The outcomes favourable to the event 'a multiple of 2 on one die and a multiple of 3 on the other die' are (2, 3), (2, 6), (4, 3), (4, 6), (6, 3) (6, 6), (3, 2), (3, 4), (3, 6), (6, 2) and (6, 4).
∴ The number of outcomes favourable to the given event = 11.
∴ Required probability =1136.
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Problems From NCERT /exemplar10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Exercise29videos
PROBABILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - POLYNOMIALSEXERCISE - Revision Exercise Long Answer Questions4videos
POLYNOMIALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRATIC EQUATIONSEXERCISE - Revision Exercise Long Answer Questions6videos
QUADRATIC EQUATIONS
Similar Questions
Two dices are thrown simultaneously. What is the probability that the sum of the numbers appearing on them is a prime number?
View SolutionTwo dice are thrown simultaneously. What is the probability that the sum of the number appearing on the dice is
(i) 7? (ii) a prime number? (iii) 1?View SolutionTwo different dice are rolled simultaneously. Find the probability that the sum of the numbers on the two dice is 10.
View SolutionTwo different dice are thrown together, find the probability that the sum of the numbers appeared is less than 5.
View SolutionTwo dice are thrown. What is the probability that the sum of the numbers appearing on the two dice is 11, it 5 appears on the first?
View SolutionTwo dice are thrown simultaneously. What is the probability of obtaining sum that is at least 12
View SolutionTwo dice are thrown randomly. What is the probability that sum of the numbers is multiple of 4?
View SolutionTwo dice are thrown simultaneously. The probability of getting the sum 2 or 8 or 12 is
View SolutionTwo dice are rolled simultaneously. What is the probability of
getting 3 on first die?View SolutionTwo dice are thrown simultaneously. Find the probability that a sum less than 7 will turn up on the upper faces.
View Solution