Triangle a plane figure formed by three non-parallel line segments is called a triangle.
Step-by-Step Text Solution:
1. Understanding the Definition of a Triangle:
A triangle is defined as a plane figure formed by three non-parallel line segments. This means that the three line segments must not run alongside each other and must connect to form a closed shape.
2. Identifying the Components of a Triangle:
The three line segments are typically referred to as the sides of the triangle. The points where these line segments meet are called the vertices of the triangle.
3. Non-Collinear Points:
A triangle can also be defined using three non-collinear points. Non-collinear points are points that do not all lie on the same straight line. When you connect these points with line segments, they form a triangle.
4. Naming the Triangle:
If we label the vertices of the triangle as A, B, and C, we can represent the triangle as triangle ABC. The notation for a triangle is typically a triangle symbol (Δ) followed by the names of the vertices.
5. Example of a Triangle:
For example, if we have three points A, B, and C that are non-collinear, we can draw line segments AB, BC, and CA. The figure formed by these line segments is triangle ABC.
A triangle is defined as a plane figure formed by three non-parallel line segments. This means that the three line segments must not run alongside each other and must connect to form a closed shape.
The three line segments are typically referred to as the sides of the triangle. The points where these line segments meet are called the vertices of the triangle.
A triangle can also be defined using three non-collinear points. Non-collinear points are points that do not all lie on the same straight line. When you connect these points with line segments, they form a triangle.
If we label the vertices of the triangle as A, B, and C, we can represent the triangle as triangle ABC. The notation for a triangle is typically a triangle symbol (Δ) followed by the names of the vertices.
For example, if we have three points A, B, and C that are non-collinear, we can draw line segments AB, BC, and CA. The figure formed by these line segments is triangle ABC.
Similar Questions
Two non - parallel line segments will always intersect.
View SolutionIn each of the following, state if the statement is true (T) or false (F): A triangle has three sides. A triangle may have four vertices. Any three line-segments make up a triangle. The interior of a triangle includes its vertices. The triangular regain includes the vertices of the corresponding triangle. The vertices of a triangle are three collinear points. An equilateral triangle is isosceles also. Every right triangle is scalene. Each acute triangle is equilateral. No isosceles triangle is obtuse.
View Solution
Knowledge Check
- Question 1 - Select One
Find the number if triangle that can be formed by joining the 6 non - collinear points on a plane .
A18B20C24D36 - Question 2 - Select One
Number of triangles that can be formed by joining the 10 non-collinear points on a plane is
A136B140C128D120
Write which of the following statement are true and which are false
(i) A simple closed figure made up of three or more line segments is called a polygon
(ii) Part of a line with two end points is called a line segment
(iii) In geometry we take a point a line and plane as undefined terms
(iv) Euclid fourth axiom says that everything equals itself
(v) The Euclidean geometry is valid only for figure in the plane
(vi) A figure formed by two rays with a common initial point is called an angleView SolutionIn each of the following, state if the statement is true (T) or false (F). A triangle has three sides A triangle may have four vertices. Any three line-segment make up a triangle The interior of a triangle includes its vertices. The triangular region includes the vertices of the corresponding triangle. The vertices of a triangle are three collinear points. An equilateral triangle is scalene. Every right triangle is scalene. Each acute triangle is equilateral. No isosceles triangle is obtuse.
View SolutionStudy the given figure and answer the following questions:
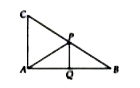
Name any two line segments inside the triangle ABC.View Solution18 points are indicated on the perimeter of a triangle ABC (see figure). If three points are choosen probability it will form a triangle. Figure 331816 (b) 12 (c) 355408 (d) 711816
View SolutionThe bases of an isosceles trapezium are 8 and 4 , and each of the non - parallel sides be produced to form a triangle ?
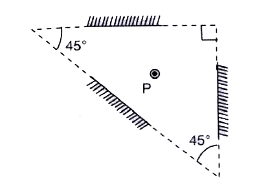
View SolutionThree plane mirrors are mounted on three walls forming an isosceles right triangle as shown in the figure. How many images are formed in all? Draw a diagram and indicate the positions of the images.
 View Solution
View Solution
