Trapezium and Parallelogram
Parallelogram
A parallelogram is a quadrilateral whose opposite sides are parallel to each other. It has four sides where the opposite angles are equal to each other. To calculate the area of a parallelogram, we need the base and height.
You have studied several different 2D shapes and sizes like a rhombus, rectangle, square, circle, etc. There are different sets of properties for all these shapes. Even the area, as well as the perimeter formulas, varies with each different shape.
Here we will discuss parallelogram along with parallelogram area formula, trapezium area, trapezium properties, and so on. We will also try to provide some examples so that things become much easier to understand.
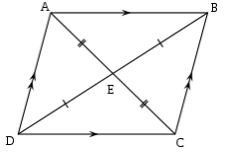
Look at the above figure of a parallelogram. Here AB//CD and AD//BC.
We can also find that AB = CD and AD = BC
And, ∠A = ∠C & ∠B = ∠D
Parallelogram Formula
In this section, the parallelogram formula has been covered. It becomes much easier for the students to solve problems by making use of these formulas.
Area of Parallelogram
The region which is occupied in a two-dimensional plan is called the area of a parallelogram. To find the area of the parallelogram, here is the formula:
Area = Base x Height
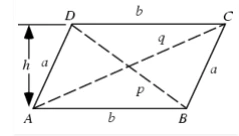
Look at the above figure where the area of the parallelogram is given by:
Area = a b sin A = b a sin B
Here, the slant length of the side of the parallelogram ABCD is ‘a’ and ‘b’ is the base.
Perimeter of Parallelogram
Regarding the perimeter of any shape, it is the total length. In the same way, the perimeter of parallelogram indicates the total distance of its boundaries. It is only possible when we know the values of its length and breadth that we can calculate the perimeter value. Its opposite sides are equal in length. So, the formula of the perimeter can be written as
Perimeter = 2 (a + b)
Properties of parallelogram
The properties of a parallelogram are:
- The opposite angles are congruent
- The opposite sides are congruent.
- The diagonals separate it into congruent.
- The two diagonals bisect each other.
- If any of the angles is a right angle, then all the other angles will be right.
- Each diagonal bisects the parallelogram into two congruent triangles.
- The consecutive angles are supplementary.
Now, we can have a look at some examples to find the area of a parallelogram. Students can get a good idea about it to solve them in the best way.
Question 1: The base and height of a parallelogram, is 6 and 9 cm respectively. Calculate its area?
Solution: Given, Base = 6 cm and Height = 9 cm.
We know, Area = Base x Height
Area = 6 × 9
Area = 54 sq.cm
So, the area of the parallelogram is 54 sq.cm
Question 2: If the base and height of a parallelogram is 4 and 7 cm, respectively. Find its area.
Solution: Given, Base = 4 cm and Height = 7 cm.
We know, Area = Base x Height
Area = 4 × 7
Area = 28 sq.cm
So, the area of the parallelogram is 54 sq.cm
Question 3: The length of diagonals of a parallelogram is 10 and 22 cm respectively, and an intersecting angle is 65 degrees. Find its area?
Solution: As we are familiar that diagonals of a parallelogram bisect each other, so the length of half the diagonal is 5 and 11 cm.
The angle which is opposite to the side b would be 180 – 65 = 115°
Now by using the law of cosines in calculating the base of the parallelogram –
b² = 5² + 11² – 2(11) (5)cos(115°)
b² = 25 + 121 – 110(-.422)
b² = 192.48
b = 13.87 cm.
So, we have found the base. Now the next thing to do is to calculate the height of the given parallelogram. For this, we need to make a calculation of the value of θ. Here we need to make use of sine law, where we get:
5/sin(θ) = b/sin(115)
θ = 19.06
Next, we need to extend the base and then draw in the height of the figure and denote it as ‘h’.
The right-angled triangle has been marked with the red line. It has the Hypotenuse of 22 cm and Perpendicular ‘h’.
So,
sin θ = h/22
where h = 7.184 cm
now, Area = base × height
A = 13.87 × 7.184
A = 99.645 sq.cm
Therefore the area of the parallelogram is 99.645sq.cm
Related Videos:
Area of Trapezium
Before we understand the area of a trapezium, it is important to know trapezium. Well, a trapezium is a quadrilateral having one set of opposite sides that are parallel. The region that a trapezium covers in a two-dimensional plane is called the area of trapezium. It is a 2 D shape, and it falls under the category of quadrilaterals. On the basis of the area and perimeter, it has its own properties. The formula of the area of trapezium is:
Area = (1/2) h (AB + CD)
Perimeter of Trapezium
The formula for the perimeter of a trapezium is:
Perimeter = Sum of all the sides = AB + BC + CD + DA
Properties of Trapezium:
Following are the properties of Trapezium:
- Two angles on the same side are supplementary, that is the sum of the angles of two adjacent sides is equal to 180°.
- The sum of angles in a trapezoid-like other quadrilateral is 360°. So in a trapezoid ABCD, ∠A+∠B+∠C+∠D = 360°.
- Its diagonals bisect with each other.
- In special cases of the isosceles trapezium, legs of the trapezium are congruent to each other. This means that despite being non-parallel, the measurement of both legs is equal.
- The length of the mid-segment is equal to 1/2 the sum of the bases. In the above figure mid-segment= 1/2 (AB+CD)
Important Chapters:


Similar Questions
State whether the statements are true (T) or (F) false.
Every trapezium is a parallelogram.View SolutionDiscussion OF Exercise-2|| Condition OF Three points be collinear|| Area OF trapezium|| Parallelogram|| Triangle || Plotting Trapezium||Rectangle||Square||Quadrilateral|| Summary
View SolutionThe opposite sides of a trapezium are parallel.
View SolutionProve, by vector method or otherwise, that the point of intersection of the diagonals of a trapezium lies on the line passing through the midpoint of the parallel sides (you may assume that the trapezium is not a parallelogram).
View SolutionParallelogram|Properties Of Parallelogram|NCERT Example
View SolutionIf D, E and F are the mid points of BC, CA and AB respectively of the △ABC then the ratio of aria parallelogram DEFB and area of the trapezium CAFD is ,
View SolutionTrapezium a quadrilateral having exactly one pair of parallel sides is called a trapezium.
View SolutionTrapezium a quadrilateral having exactly one pair of parallel sides is called a trapezium.
View SolutionParallelogram|Properties Of A Parallelogram
View SolutionProve that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of trapezium and is half of their difference.
View Solution


