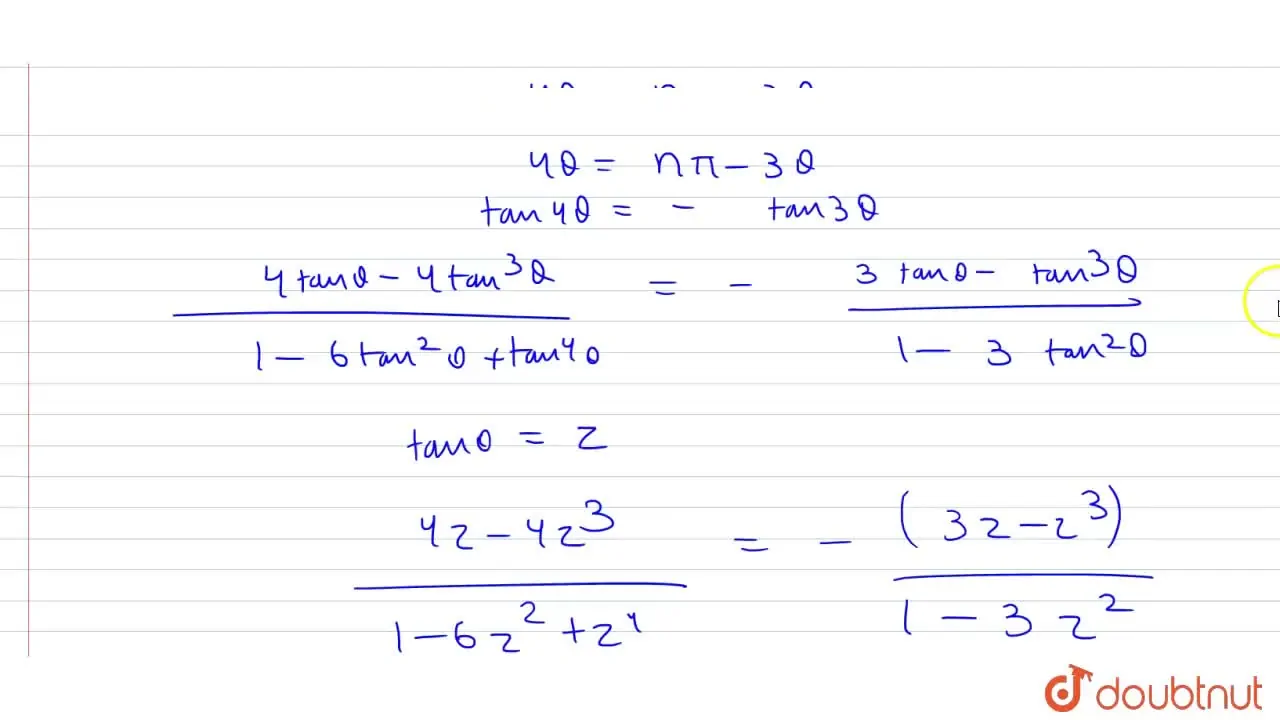To find the sum sin22π7+sin24π7+sin28π7, we follow the following method.
Put 7θ=2nπ, where n is any integer. Then
sin4θ=sin(2nπ−3θ)=−sin3θ
This means that sinθ takes the values 0,±sin(2π/7),±sin(2π/7),±sin(4π/7),and±sin(8π/7).
From Eq. (i), we now get
2sin2θcos2θ=4sin3θ−3sinθ
or 4sinθcosθ(1−2sin2θ)=sinθ(4sin2θ−3)
Rejecting the value sinθ=0, we get
4cosθ(1−2sin2θ)=4sin2θ−3
or 16cos2θ(1−2sin2θ)2=(4sin2θ−3)2
or 16(1−sin2θ)(1−4sin2θ+4sin4θ)
=16sin4θ−24sin2θ+9
or 64sin6θ−112sin4θ−56sin2θ−7=0
This is cubic in sin2θ with the roots sin2(2π/7),sin2(4π/7),andsin2(8π/7).
The sum of these roots is
sin22π7+sin24π7+sin28π7=11264=74.
The value of (tan2π7+tan22π7+tan23π7)×(cot2π7+cot22π7+cot23π7) is
A
105
B
35
C
210
D
none of these.
Video Solution
Text Solution
The correct Answer is:A
Let θ=nπ7 (so that 7θ=nπ), n∈Z
⇒4θ+3θ=nπ
or4θ=tan(nπ−3θ)=−tan3θ
or 4tanθ−4tan3θ1−6tan2θ+tan4θ=−3tanθ−tan3θ1−3tan2θ
or 4z−4z31−6z2+z4=−3z−z31−3z2 [where tanθ=z (say)]
or (4−4z2)(1−3z2)=−(3−z2)(1−6z2+z4)
or z6−21z4=35z2−7=0 ... (i)
This is a cubic equation in z2, i.e., in tan2θ.
The roots of this equation are therefore
tan2π/7,tan22π/7,andtan23π/7. From Eq. (i),
Sum of the roots =−(−21)1=21
⇒tan2π7+tan22π7+tan23π7=21 ...(ii)
Putting 1/y in place of z in Eq. (i), we get
−7y6+35y4−21y2+1=0
or7y6−35y4+21y2−1=0 ...(iii)
This is a cubic equation in y2, i.e., in cot2θ.
The roots of this equation are therefore cot2π/7,cot22π/7,andcot23π/7.
Sum of the roots of Eq. (iii) = 357=5
⇒cot2π7+cot22π7+cot23π7=5 ...(iv)
By multiplying Eqs. (ii) and (iv), we get
(tan2π7+tan22π7+tan23π7)(cot2π7+cot22π7+cot23π7)
=21×5=105
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Exercise (Matrix Match Type )9videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Exercise (Numerical)38videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Exercise (Multiple)22videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE38videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS EXERCISE - Multiple Correct Answers Type6videos
TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS
Similar Questions
The value of sin2π7+sin4π7+sin8π7, is
View Solutionsin2π8+sin2(3π)8+sin2(5π)8+sin2(7π)8=?
View SolutionFind the value of : sin2(π18)+sin2(π9)+sin2(7π18)+sin2(4π9)
View SolutionFind the value of sin(π7)sin(2π7)sin(4π7)=
View SolutionThe value of sinπ7+sin2π7+sin3π7 is
View Solutionsin(π7)sin(2π7)sin(3π7)
View Solutionsin4π8+sin43π8+sin45π8+sin47π8 is equal to
View Solutionthe value of sin(π7)+sin(2π7)+sin(3π7) is
View Solutionsin2(π)4+sin2(3π)4+sin2(5π)4+sin2(7π)4=2
View SolutionThe value of sinπ7sin2π7sin3π7, is
View Solution