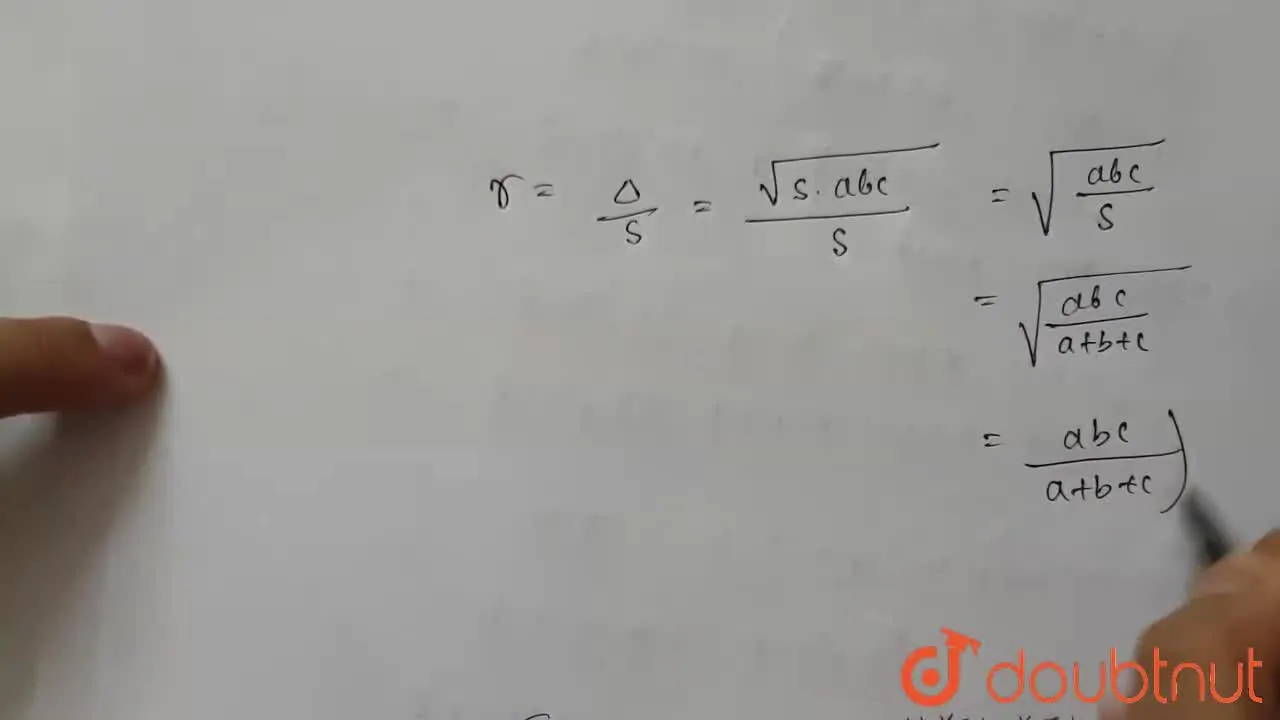Three circles whose radii are a,b and c and c touch one other externally and the tangents at their points of contact meet in a point. Prove that the distance of this point from either of their points of contact is (abca+b+c)12.
Step by step video & image solution for Three circles whose radii are a,b and c and c touch one other externally and the tangents at their points of contact meet in a point. Prove that the distance of this point from either of their points of contact is ((abc)/(a+b+c))^(1/2). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Three circles touch each other externally. The tangents at their point of contact meet at a point whose distance from a point of contact is 4. Then, the ratio of their product of radii to the sum of the radii is
View SolutionThree circles touch each other externally. The tangents at their point of contact meet at a point whose distance from a point of contact is 4. Then, the ratio of their product of radii to the sum of the radii is
View SolutionThree circles with radius r1,r2,r3 touch one another externally. The tangents at their point of contact meet at a point whose distance from a point of contact is 2. The value of (r1r2r3r1+r2+r3) is equal to
View Solution3 circles of radii a,b,c(a<b<c) touch each other externally and have x-axis as a common tangent then
View SolutionCircles with radii 3, 4 and 5 touch each other externally. If P is the point of intersection of tangents to these circles at their points of contact, then if the distance of P from the points of contact is λ then λ2 is _____
View SolutionCircles of radii 3,4,5 touch each other externally . Let P be the point of intersection of tangents of these circles at their points of contact .Show that the distance of P from a point of contact is √5.
View SolutionTwo circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
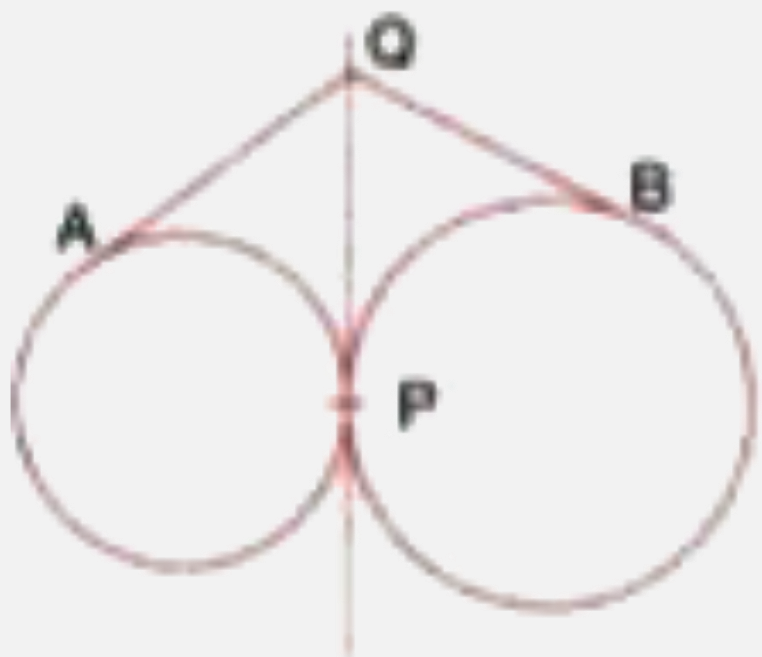 View Solution
View SolutionProve that the tangent at any point of circle is perpendicular to the radius through the point of contact.
View SolutionProve that the tangent at any point of circle is perpendicular to the radius through the point of contact.
View SolutionIf a circle, whose centre is (-1,1) touches the straight line x+2y = 12, then the co-ordinates of the point of contact are
View Solution