There are two die A and B both having six faces. Die A has three faces marked with 1, two faces marked with 2, and one face marked with 1, two faces marked with 2, and one face marked with 3. Die B has one face marked with 1, two faces marked with 2, and three faces marked with 3. Both dices are thrown randomly once. If E be the event of getting sum of the numbers appearing on top faces equal to x and let P(E) be the probability of event E, then
When x = 4, then P(E) is equal to
5/9
6/7
7/18
8/19
The correct Answer is:C
The number of ways in which different sums can occurs is (3 + 2 + 1)(1 + 2 + 3) = 36. The probability of 4 is 14/36=7/18.
Related Playlists
- BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Matrix)2videos
PROBABILITY I
- BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Numerical)7videos
PROBABILITY I
- BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Multiple)8videos
PROBABILITY I
- BOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank37videos
PROBABILITY AND STATISTICS
- BOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - NUMARICAL VALUE TYPE2videos
PROBABILITY II
Similar Questions
There are two die A and B both having six faces. Die A has three faces marked with 1, two faces marked with 2, and one face marked with 3. Die B has one face marked with 1, two faces marked with 2, and three faces marked with 3. Both dices are thrown randomly once. If E be the event of getting sum of the numbers appearing on top faces equal to x and let P(E) be the probability of event E, then P(E) is maximum when x equal to
View SolutionThere are two die A and B both having six faces. Die A has three faces marked with 1, two faces marked with 2, and one face marked with 3. Die B has one face marked with 1, two faces marked with 2, and three faces marked with 3. Both dices are thrown randomly once. If E be the event of getting sum of the numbers appearing on top faces equal to x and let P(E) be the probability of event E, then P(E) is minimum when x equals to
View SolutionA dice marked with digit {1,2,2,3,3,3}, thrown three times, then the probability of getting sum of number on face is six, is equal to ;- 7216
View SolutionThe mean of the numbers obtained on throwing a die having written 1 one three faces, 2 on two faces and 5 on one face is
View SolutionA six-faced unbiased die is thrown twice and the sum of the numbers appearing on the upper face is observed to be 7. The probability that the number 3 has appeared atleast once, is
View SolutionA six -faced unbiased die is thrown twice and the sum of the numbers appearing on the upper face is observed to be7. The probability that the number 3 has appeared at least one ,is
View SolutionA ordinary cube has four plane faces, one face marked 2 and another face marked 3, find the probability of getting a total of 7 in 5 throws.
View SolutionA dice has four blank faces and two faces marked 3. The change of getting a total of 12 in 5 throws is
View SolutionThe net shown below can be folded into the shape of a cube. The face marked with the letter L is opposite to the face marked with which letter?
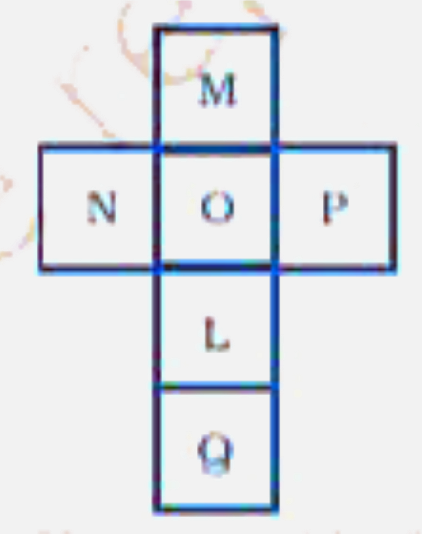 View Solution
View SolutionD1,D2 are two cubical dice, with faces of D1 marked 1,2,2,3,3,3 and faces of D2 marked 1,1,2,2,3,3. One of the 2 dice is selected at random and tosses 3 times. If the sum of the numbers obtained is equal to 6 then the probability that the selected die is D1 is
View Solution


