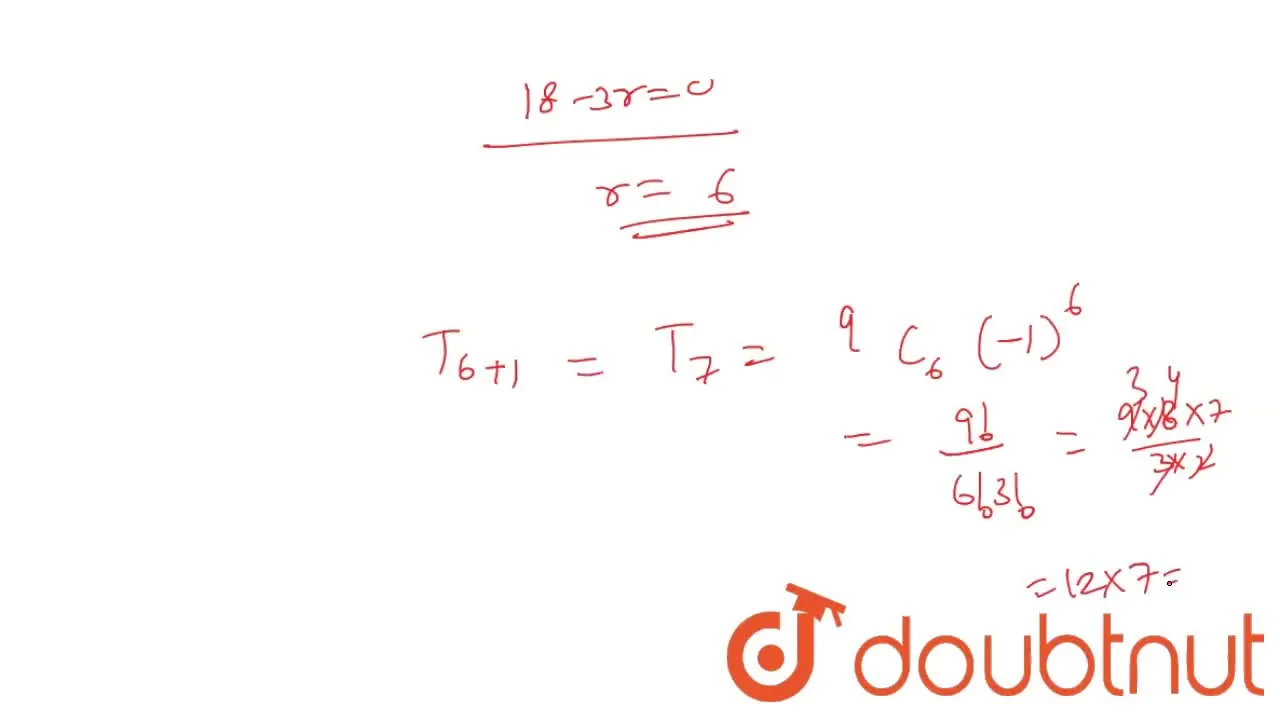The value of the term independent of x in the expansion of (x2−1x)9 is :
A
9
B
18
C
48
D
84
Video Solution
Text Solution
The correct Answer is:D
(x2−1x)9
tr+1=.9Cr(x2)9−r(−1x)r
.9Crx18−2r.(−1)r.x−r
=.9Cr(x)18−3r(−1)r ...(1) Term will be independent of x when
18 - 3r = 0
r = 6
Put r = 6, in [1]
t7=.9C6(−1)6=9!6!3!=84
|
Updated on:21/07/2023
Related Playlists
Similar Questions
The term independent of x in the expansion of (x2−13x)9 is
View SolutionTerm independent of x in the expansion of (3x2−13x)9.
View SolutionFind the term independent of x in the expansion of: (x−1x)14 .
View SolutionThe term independent of x in the expansion of (x−1x)12 is
View SolutionThe term independent of x in the expansion of (1+x)n(1−1x)n is
View SolutionThe term independent of x in the expansion of (32x2−13x)9 is
View SolutionThe term independent of x in the expansion of (1+2x+2x)3 is
View SolutionThe term independent of x in the expansion of (x2−1/3x)9 is equal to
View SolutionFind the term independent of x in the expansion of: (2x2−3x3)10.
View SolutionThe term independent of x in the expansion of (2x+13x)6 is
View Solution