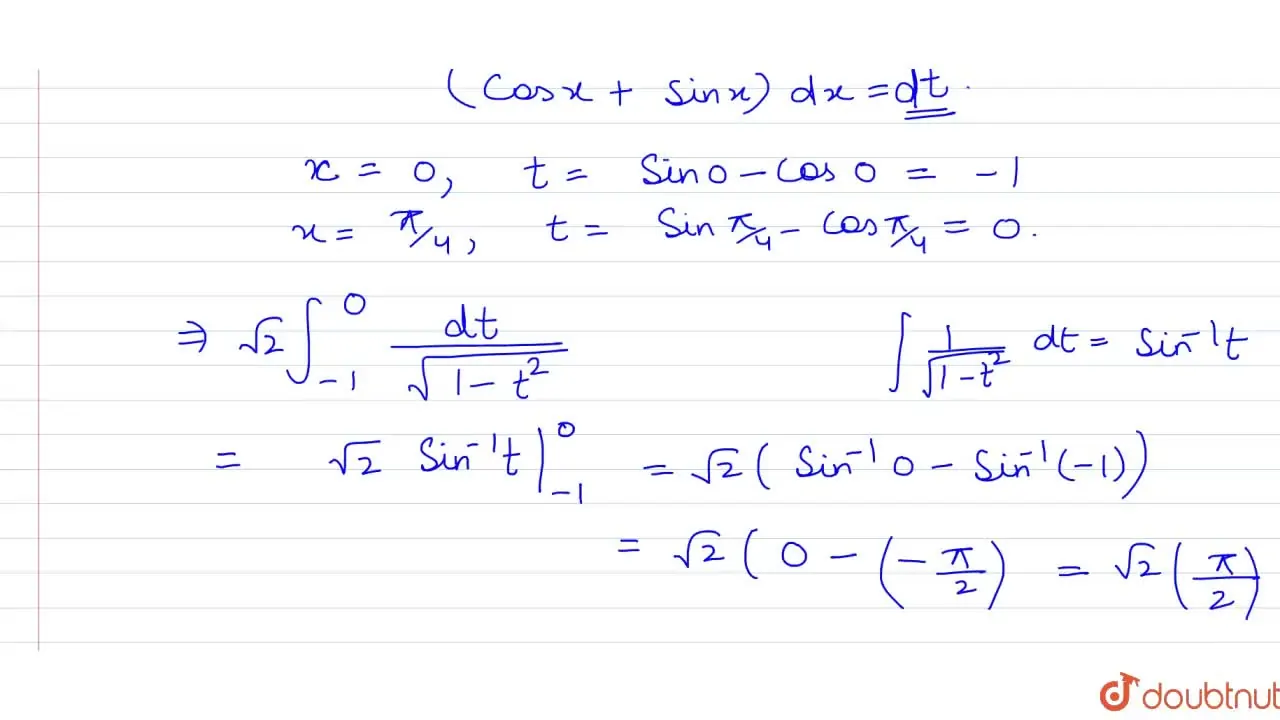The value of ∫π40√tanxdx+∫π40√cotxdxis equal to
A
π4
B
π2
C
π2√2
D
π√2
Video Solution
Text Solution
The correct Answer is:D
∫π40√tanxdx+∫π40√cotx.dx
=∫π40(√tanx+√cotx)dx
=∫π40(√sinx√cosx+√cosx√sinx)dx
=∫π40(sinx+c⊗0√sinx.√cosx.dx
=√2∫π40(sinx+cosx)(√1−(sin2x+cos2x−2sinxcosx)).dx
Put sinx−cosx=t⇒(cosx+sinx)dx=dt
When x=0,t=−1 and x=π4,t=0
=√2∫0−11√1−t2.dt=√2(sin−1t)0−1
=√2[sin−1(0)−sin−1(−1)]
=√2[0−(−π2)]
=π√2.
|
Updated on:21/07/2023
Related Playlists
- BOOK - NDA PREVIOUS YEARSCHAPTER - DEFINITE INTEGRATION & ITS APPLICATIONEXERCISE - DIRECTIONS60videos
DEFINITE INTEGRATION & ITS APPLICATION
- BOOK - NDA PREVIOUS YEARSCHAPTER - CONICS - PARABOLA, ELLIPSE & HYPERBOLAEXERCISE - MATH62videos
CONICS - PARABOLA, ELLIPSE & HYPERBOLA
- BOOK - NDA PREVIOUS YEARSCHAPTER - DERIVATIVESEXERCISE - MCQs94videos
DERIVATIVES
Similar Questions
The value of ∫π/40√tanxdx+∫π/40√cotxdx is equal to
View Solution∫π/40√cotxdx=?
View Solution∫π40√tanxdx
View Solution∫π/40√1+cos2xdx
View Solution∫π/30[√3tanx]dx=
View Solution∫π2/40sin√xdx equals to
View SolutionThe value of ∫−π/401+tanx1−tanxdx is
View Solution∫π/20log(cotx)dx=
View Solution∫π40√1+sin2xdx
View SolutionWhat is ∫π20ln(tanx)dx equal to ?
View Solution