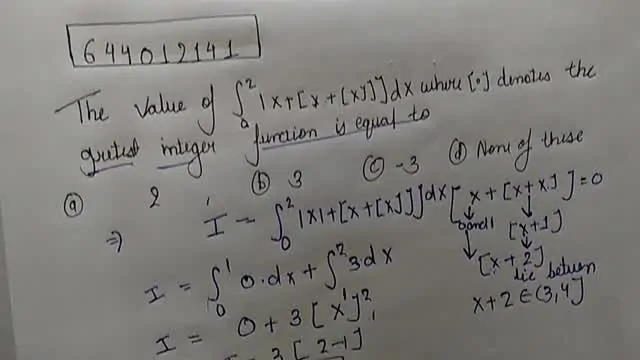The value of ∫20[x+[x+[x]]]dx (where, [.] denotes the greatest integer function )is equal to
2
3
−3
None of these
The correct Answer is:B
Step by step video & image solution for The value of int_(0)^(2)[x+[x+[x]]] dx (where, [.] denotes the greatest integer function )is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise For Session 420videos
DEFINITE INTEGRAL
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise For Session 520videos
DEFINITE INTEGRAL
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise For Session 214videos
DEFINITE INTEGRAL
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)7videos
COORDINATE SYSTEM AND COORDINATES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - DETERMINANTS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
DETERMINANTS
Similar Questions
The value of ∫20[x2−x+1]dx (where , [.] denotes the greatest integer function ) is equal to
View Solution∫2π0[|sinx|+|cosx|]dx, where [.] denotes the greatest integer function, is equal to :
View SolutionThe value of ∫x0[t+1]3dt (where, [.] denotes the greatest integer function of x) is qeual to
View SolutionLtx→2 [x] where [⋅] denotes the greatest integer function is equal to
View SolutionThe value of ∫3−1{|x−2|+[x]}dx, where [.] denotes the greatest integer function, is equal to
View SolutionThe value of ∫10π0[tan−1x]dx (where, [.] denotes the greatest integer functionof x) is equal to
View SolutionThe value of ∫∞0[2e−x]dx (where ,[.] denotes the greatest integer function of x) is equal to
View Solutionthe value of ∫[x]0dx (where , [.] denotes the greatest integer function)
View Solution∫2−1[[x]1+x2]dx, where [.] denotes the greatest integer function, is equal to
View SolutionThe value of l =∫30([x]+[x+13]+[x+23])dx where [.] denotes the greatest integer function is equal to
View Solution