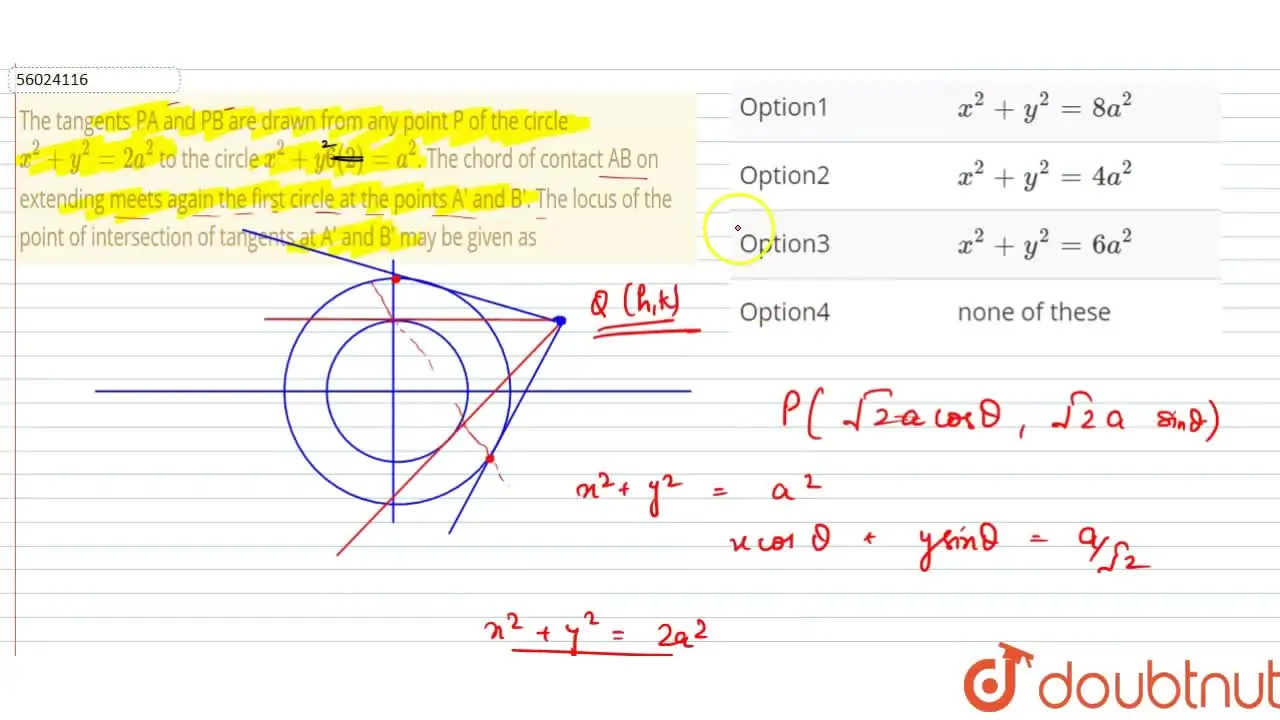
The tangents PA and PB are drawn from any point P of the circle x2+y2=2a2 to the circle x2+y2=a2. The chord of contact AB on extending meets again the first circle at the points A' and B'. The locus of the point of intersection of tangents at A' and B' may be given as
x2+y2=8a2
x2+y2=4a2
x2+y2=6a2
none of these
The correct Answer is:A
The equation of the chord of contact of tangents drawn from any point P(√2acosθ,√2acosθ) to the circle x2+y2=a2 is
xcosθ+ysinθ=a√2 ...(i)

Let Q(h, k) be the point of intersection of tangents to the circle x2+y2=2a2 at A' and B'. Then, the equation of the chord of contact A' B' is
hx+ky=2a2 ...(ii)
Clearly (i) and (ii) represent the same line.
∴cosθh=sinθk=12√2a
⇒cosθ=h2√2a,sinθ=k2√2a
⇒h28a2+k28a2=1⇒h2+k2=8a2
Hence, the locus of (h, k) is x2+y2=8a2
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)1videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type12videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test55videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test31videos
CARTESIAN PRODUCT OF SETS AND RELATIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test59videos
COMPLEX NUMBERS
Similar Questions
If two tangents are drawn from a point to the circle x2+y2=32 to the circle x2+y2=16, then the angle between the tangents is :
View SolutionIf two tangents are drawn from a point to the circle x2+y2=32 to the circle x2+y2=16, then the angle between the tangents is
View SolutionIf from any point on the circle x2+y2=a2 tangents are drawn to the circle x2+y2=b2,(a>b) then the angle between tangents is
View SolutionTangents are drawn from any point on circle x2+y2−4x=0 to the circle x2+y2−4x+2=0 then angle between tangents is:
View SolutionIf the chord of contact of tangents from a point P(h, k) to the circle x2+y2=a2 touches the circle x2+(y−a)2=a2, then locus of P is
View SolutionIf the tangents are drawn from any point on the line x+y=3 to the circle x2+y2+9, then the chord of contact always passes through fixed point. Find that point
View SolutionThe length of the tangent drawn from any point on the circle x2+y2+2gx+2fy+a=0 to the circle x2+y2+2gx+2fy+b=0 is
View SolutionTangents are drawn from any point on the hyperbola x29−y24=1 to the circle x2+y2=9. Find the locus of mid point of the chord of contact.
View SolutionTangents are drawn from any point on the hyperbola x29−y24=1 to the circle x2+y2=9 . Find the locus of the midpoint of the chord of contact.
View SolutionTangents PAandPB are drawn to the circle x2+y2=8 from any arbitrary point P on the line x+y=4. The locus of mid-point of chord of contact AB is
View Solution