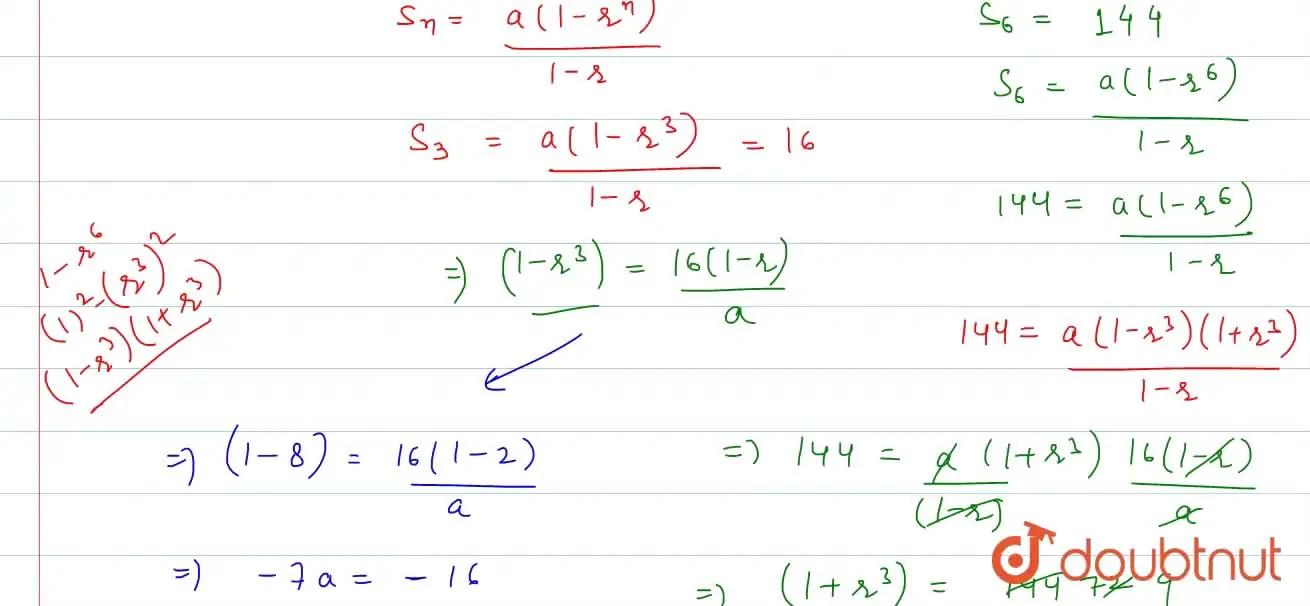The sum of first three terms of a G.P is 16 and the sum of the next three terms is 128. Determine the first term, the common ratio and the sum to n terms of the G.P.
The correct Answer is:N/a
Let first term be 'a' and common ratio 'r' Now S3=1
⇒a(1−r3)1−r=16….(1)
andS6=16+128
⇒a(1−r6)1−r=144
⇒a(1−r3)1−r⋅(1+r3)=144
⇒16⋅(1+r3)=144
⇒1+r3=9
⇒r3=8
⇒r=2
Now a(1−r3)1−r=16 [Put r=2 in equation (1)]
⇒a(1−8)1−2=16
⇒a=167
and Sn=a(rn−1)r−1
Sn=167(2n−1)2−1=167(2n−1)
∴a=167,r=2,Sn=167(2n−1)
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9.410videos
SEQUENCE AND SERIES
- BOOK - NAGEEN PRAKASHANCHAPTER - SEQUENCE AND SERIESEXERCISE - Miscellaneous Exercise32videos
SEQUENCE AND SERIES
- BOOK - NAGEEN PRAKASHANCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9.218videos
SEQUENCE AND SERIES
- BOOK - NAGEEN PRAKASHANCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE12videos
RELATIONS AND FUNCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - SETSEXERCISE - MISC Exercise16videos
SETS
Similar Questions
The sum of first three terms of a G.P. is 16 and the sum of the next three terms is 128. Determine the first term, the common ratio and the sum to n terms of the GP.
View SolutionThe sum of first three terms of a G.P. is 15 and sum of next three terms is 120. Find the sum of first n terms.
View SolutionThe sum of first three terms of a G.P is 7 and the sum of their squares is 21. Determine the first five terms of the G.P.
View SolutionThe sum of first three terms of a G.P. is 18 of the sum of the next three terms. Find the common ratio of G.P.
View SolutionThe sum of the first thre consecutive terms of G.P is 13 and the sum of their squares is 91. Determine the G.P.
View SolutionThe sum of first two terms of a G.P. is 53 and the sum to infinity of the series is 3. Find the first term :
View SolutionThe sum of first three terms of a G.P. is 21 and sum of their squares is 189. Find the common ratio :
View SolutionThe sum of first two terms of a G.P. is 53 and the sum to infinity of the series is 3. Find the first term :
View SolutionThe sum of the first 2n terms of an A.P. is x and the sum of the next n terms is y, its common difference is :
View SolutionThe sum of the first three terms of an A.P. is 9 and the sum of their squares is 35. The sum to first n terms of the series can be
View Solution