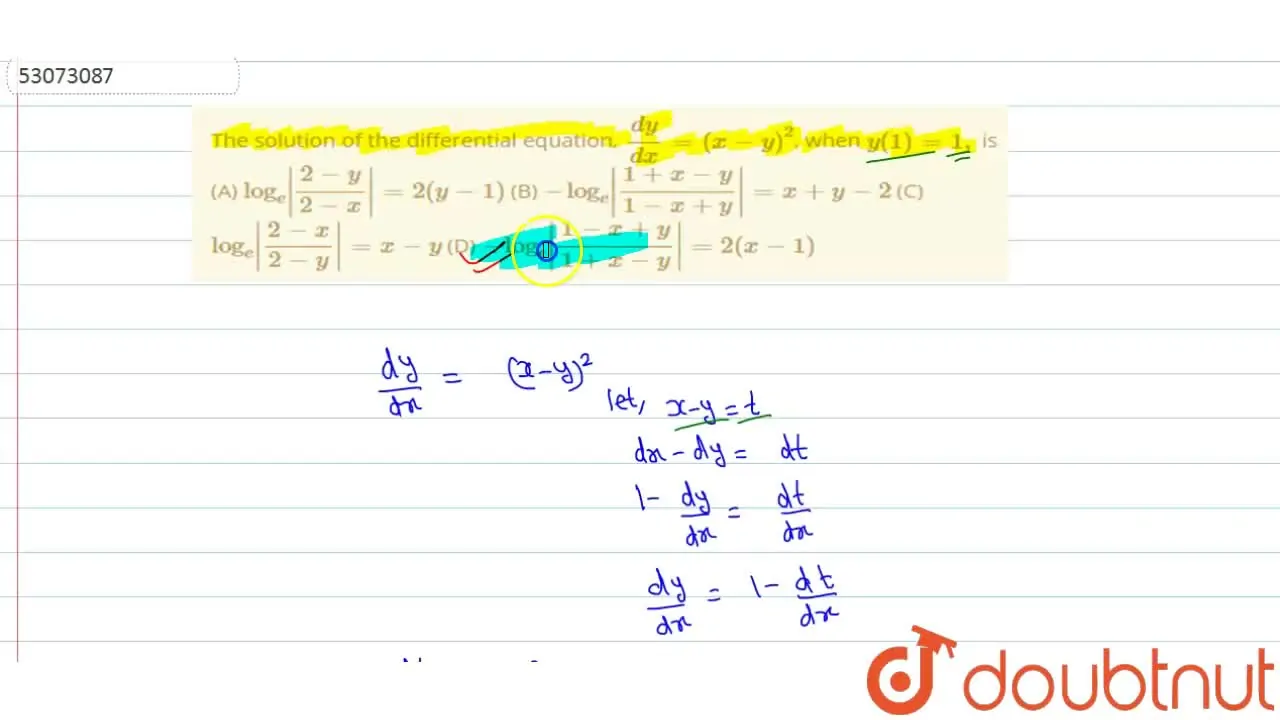
The solution of the differential equation, dydx=(x−y)2, when y(1)=1, is
loge∣∣∣2−y2−x∣∣∣=2(y−1)
−loge∣∣∣1+x−y1−x+y∣∣∣=x+y−2
loge∣∣∣2−x2−y∣∣∣=x−y
−loge∣∣∣1−x+y1+x−y∣∣∣=2(x−1)
The correct Answer is:D
We have dydx=(x−y)2 which is a differential equation of
the form
dydx=f(ax+by+c)
Put x−y=t
⇒1−dydx=dtdx⇒dydx=1−dtdx
⇒1−dtdx=t2[∴dydx=(x−y)2]
⇒dtdx=1−t2⇒∫dt1−t2=∫dx
[separating the variables]
⇒12loge(1+t1−t)=x+C
[∫dxa2−x2=12aloge∣∣∣a+xa−x∣∣∣+C]
⇒12loge(1+x−y1−x+y)=x+C[∴t=x−y]
Since, y=1 when x=1, therefore
12loge(1+01+0)=1+C
⇒C=−1[∴log1=0]
∴12loge(1+x−y1−x+y)=x+1
⇒−loge∣∣∣1−x+y1+x−y∣∣∣=2(x−1)
[∴log1x=logx−1=−logx]
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - DIFFERENTIAL EQUATIONS EXERCISE - TOPIC 1 SOLUTION OF DIFFERENTIAL EQUATIONS BY VARIABLE <br> SEPARATION METHOD <br> OBJECTIVE QUESTIONS II (ONE OR MORE THAN ONE CORRECT OPTION)1videos
DIFFERENTIAL EQUATIONS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - DIFFERENTIAL EQUATIONS EXERCISE - TOPIC 1 SOLUTION OF DIFFERENTIAL EQUATIONS BY VARIABLE <br> SEPARATION METHOD <br>OBJECTIVE QUESTIONS II (ONE OR MORE THAN ONE CORRECT OPTION)7videos
DIFFERENTIAL EQUATIONS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - DEFINITE INTEGRATIONEXERCISE - LIMITS AS THE SUM6videos
DEFINITE INTEGRATION
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - ELLIPSEEXERCISE - EQUATION OF CHORD OF CONTACT, CHORD BISECTED AT A GIVEN POINT & DIAMETER3videos
ELLIPSE
Similar Questions
The solution of the differential equation dydx=(x−y)2, then y(1)=1, is
View SolutionThe solution of the differential equation dydx=(4x+y+1)2 , when y(0)=1 is
View SolutionThe solution of the differential equation dydx=1x+y2 is
View SolutionThe solution of the differential equation dydx=(4x+y+1)2, is
View SolutionThe solution of the differential equation dydx−ex−y=1 is
View SolutionThe solution of the differential equation xdydx+y=y2 is
View SolutionSolution of the differential equation dydx=x2y+y is
View SolutionSolution of the differential equation ydx+(x−y2)dy=0 is
View SolutionThe solution of the differential equation dydx=(1+x)(1+y2) is -
View SolutionThe solution of the differential equation dydx=1x+y2 is
View Solution