The smallest value of k, for which both the roots of the equation, x2−8kx+16(k2−k+1)=0 are real, distinct and have values at least 4, is
6
4
2
0
The correct Answer is:D
Let f(x)=x2−8kx+16(k2−k+1) brgt 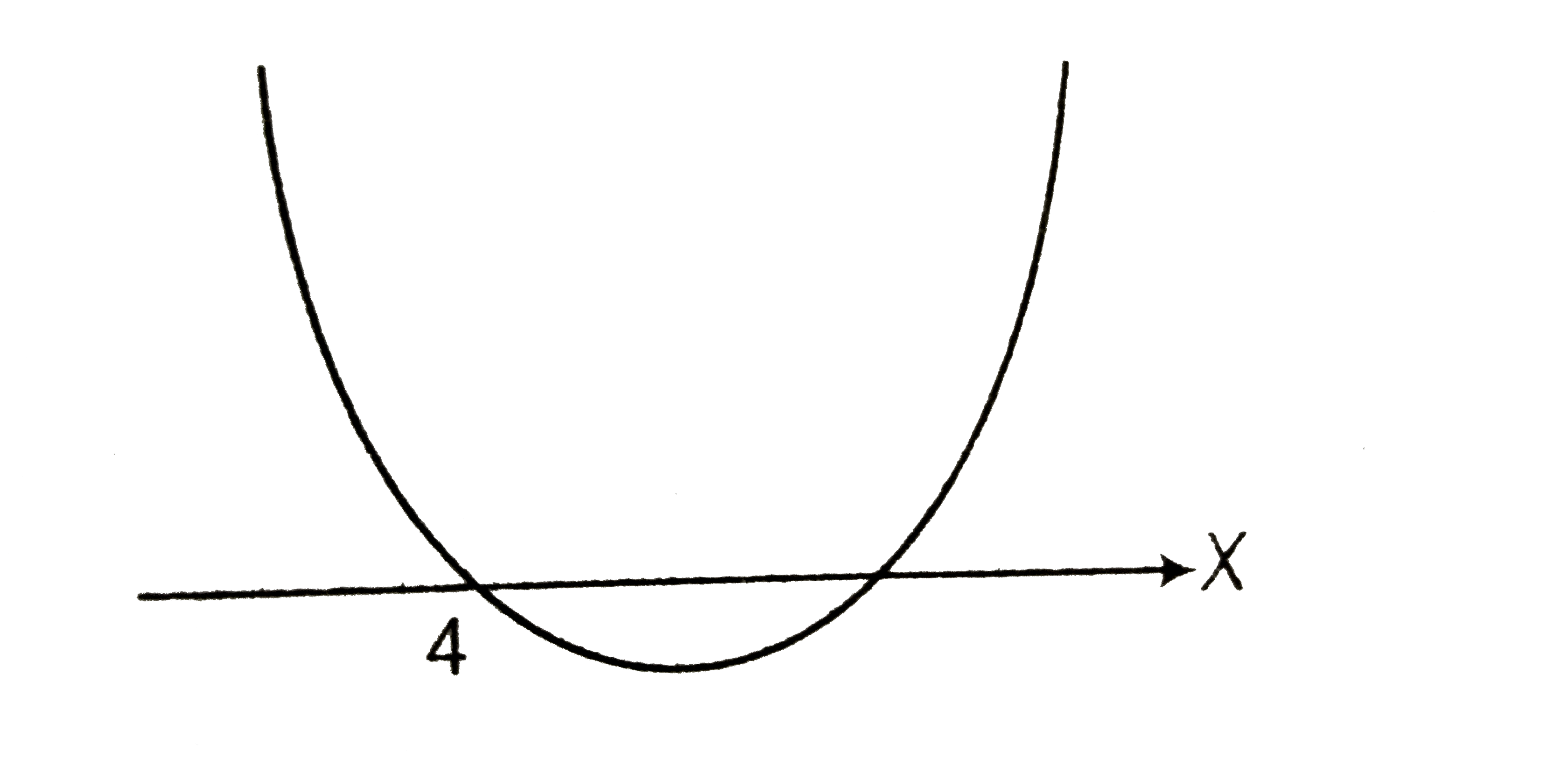
∴D>0
⇒64k2−4.16(k2−k+1)>0
⇒k>1 …….i
⇒−b2a>4⇒8k2>4
⇒k>1………….ii
and f(4)≥0
⇒16−32k+16(k2−k+1)≥0
⇒k2−3k+2≥0
⇒(k−1)(k−2)≥0
k≤1 or k≥2...........iii
From Eqs i, ii and iii we get
k≥2
kmin=2
Related Playlists
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Subjective Type Questions)24videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)17videos
THE STRAIGHT LINES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam2videos
THREE DIMENSIONAL COORDINATE SYSTEM
Similar Questions
The number of values (s) of k , for which both the roots of the equation x2−6kx+9(k2−k+1)=0 are real, distinct and have values atmost 3 is ________
View SolutionThe least value of k which makes the roots of the equation x2+5x+k=0 imaginary is
View SolutionThe value of k for which the equation (k−2)x2+8x+k+4=0 has both roots real, distinct and negative, is
View SolutionIf the roots of the quadratic equation x2+4x+k=0 are real, then the value of k is:
View SolutionIf the equation 3x2−6x+k=0 has real and distinct roots, then the value of k is
View SolutionThe value of k for which the sum of the squares of the roots of 2x2−2(k−2)x−k=0 is least is
View SolutionIF both the roots of the quadratic equation x2−2kx+k2+k−5=0 are less than 5, then k lies in the interval
View SolutionIf the roots of the quadratic equation 2x2+8x+k=0 are equal, find the value of k.
View SolutionThe value of k for which the equation x2+3kx+(k2−k+2)+0 has equal roots, is:
View SolutionIf the equation 2x3−6x+k=0 has three real and distinct roots, then find the value (s) of k.
View Solution


