The position vectors of the vertices A,B and C of a triangle are ˆi−ˆj−3ˆk,2ˆi+ˆj−2ˆk and −5ˆi+2ˆj−6ˆk, respectively. The length of the bisector AD of the ∠BAC, where D is on the segment BC, isSolution in Punjabi
34√3
14
112
None of these
The correct Answer is:A

|AB|=∣∣(2ˆi+ˆj−2ˆk)−(ˆi−ˆj−3ˆk)∣∣
=∣∣ˆi+2ˆj+ˆk∣∣
=√12+22+12=√6
|AC|=∣∣(−5ˆi+2ˆj−6ˆk)−(ˆi−ˆj−3ˆk)∣∣
=∣∣−6ˆi+3ˆj−3ˆk∣∣
=√(6−6)2+32+(−3)2=√54=3√6
BD:DC=AB:AC=√63√6=13
∴Position vector of D=1(−5ˆi+2ˆj−6ˆk)+3(2ˆi+ˆj−2ˆk)1+3
=14(ˆi+5ˆj−12ˆk)
∴AD=Position vector of D-position vector of A
AD=14(ˆi+5ˆj−12ˆk)−(ˆi−ˆj−3ˆk)=14(−3ˆi+9ˆj)
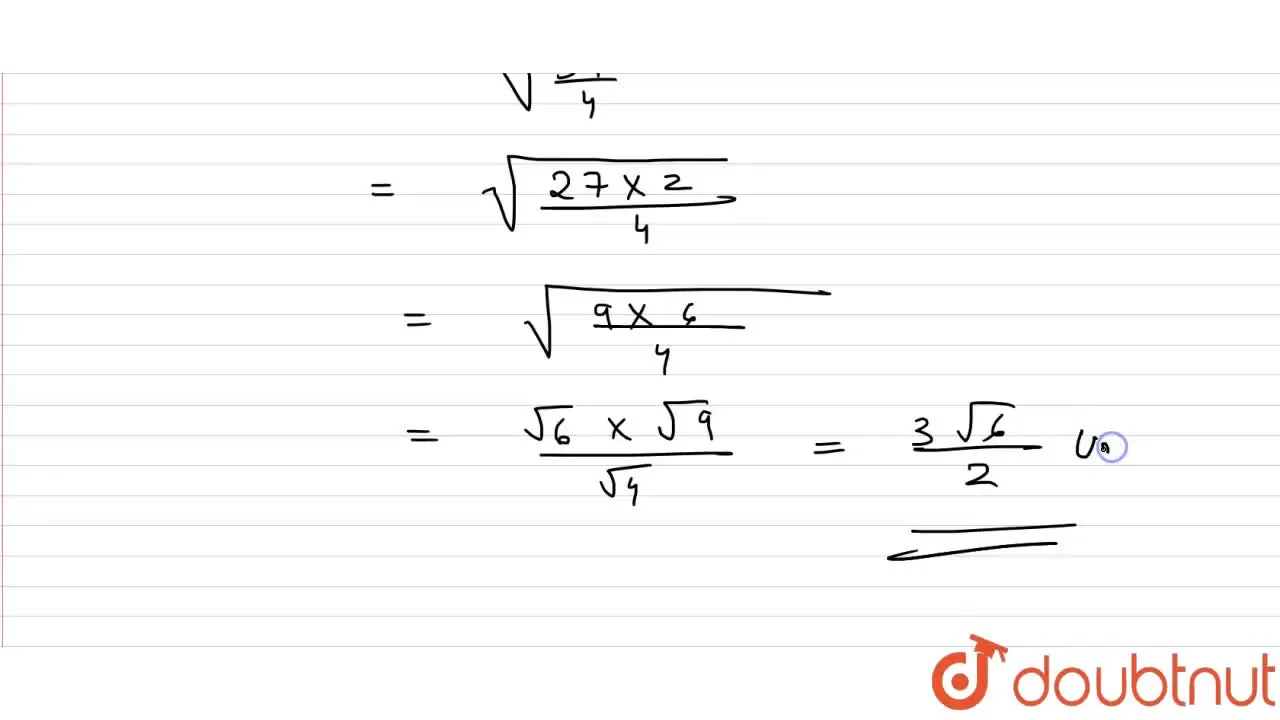
=34(−ˆi+3ˆj)
|AD|=34√(−1)2+32=34√10
Related Playlists
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 17videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 217videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
TRIGONOMETRIC FUNCTIONS AND IDENTITIES
Similar Questions
Classify the following measure as scalar and vector: 10Kg
04:29View SolutionIf a=2ˆi−ˆj+2ˆkandb=−ˆi+ˆj−ˆk, then find a+b. Also, find a unit vector along a+b.
03:12View SolutionLet αandβ be non-zero real numbers such that 2(cosβ−cosα)+cosαcosβ=1. Then which of the following is/are true ?
04:09View SolutionThe unit vector which is orthogonal to the vector 5ˆi+2ˆj+6ˆk and is coplanar with vectors 2ˆi+ˆj+ˆkandˆi−ˆj+ˆkis
09:50View SolutionIf the position vector of the vertices A,B and C of a ΔABC be (ˆi+2ˆj+3ˆk),(2ˆi+3ˆj+ˆk) and (3ˆi+ˆj+2ˆk) respectively, prove that ΔABC is equilateral.
04:14View Solutionयदि बिन्दुओं A, B तथा C के स्थिति सदिश क्रमश: ˆi+2ˆj+3ˆk,−ˆi−ˆj+8ˆk तथा −4ˆi+4ˆj+6ˆk हैं तो सिद्ध कीजिए कि- ABC एक समबाहु त्रिभुज हैं |
11:29View Solutionसदिशों 2ˆi+ˆj+ˆk तथा ˆi−ˆj+ˆk के तल में और 5ˆi+2ˆj+6ˆk के लम्भिक एक इकाई सदिश है
04:00View Solutionउस त्रिभुज का क्षेत्रफल ज्ञात करें जिसके शीर्षों के स्थिति सदिश ˆi+ˆj+2ˆk,2ˆi+2ˆj=3ˆk तथा 3ˆi−ˆj−ˆk हैं |
View SolutionThe position vectores of the vertices A,B, C of a △ABC areˆi−ˆj−3ˆk,2ˆi+ˆj−2ˆkand−5ˆi+2ˆj−6ˆk respectively. The length of the bisector AD of the angle ∠BAC, where D is on the line segments BC, is
View Solutionसिद्ध कीजिए कि वह त्रिभुज जिसके शीर्षों के स्थिति सदिश क्रमश : ˆi+2ˆj+3ˆk,2ˆi+3ˆj+ˆk और 3ˆi+ˆj+2ˆk है , एक समबाहु त्रिभुज है ।
View SolutionThe position vectores of the vertices A,B, C of a delta ABC areˆi−ˆj−3ˆk,2ˆi+ˆj−2ˆkand−5ˆi+2ˆj−6ˆk respectively. The length of the bisector AD of the angle ∠BAC, where D is on the line segments BC, is
06:01View SolutionThe position vectors of the vertices A,B,C of a △ABC are ˆi−ˆj−3ˆk,2ˆi+ˆj−2ˆk and −5ˆi+2ˆj−6ˆk respectively . The length of the bisector AD of the angle ∠BAC where D is on the line segment BC, is : -
View SolutionThe position vectors of the vertices A,B,C of ΔABC are ˆi−ˆj−3ˆk,2ˆi+ˆj−2ˆk and −5ˆi+2ˆj−6ˆk respectively. The length of the bisector AD of the angle ∠BAC where D is on the line segment BC is
View SolutionA unit vector is orthogonal to 5ˆi+2ˆj+6ˆk and is coplanar to 2ˆi+ˆj+ˆkandˆi−ˆj+ˆk then the vector is
05:30View SolutionThe area of the triangle formed by the points where position vector are 3ˆi+ˆj,5ˆi+2ˆj+ˆkandˆi−2ˆj+3ˆk is :
05:21View SolutionVertices of a triangle are given by hati+3hatj+2hatk, 2hati-hatj+hatk and -hati+2hatj+3hatk , then area of triangle is (in units)
09:01View Solution