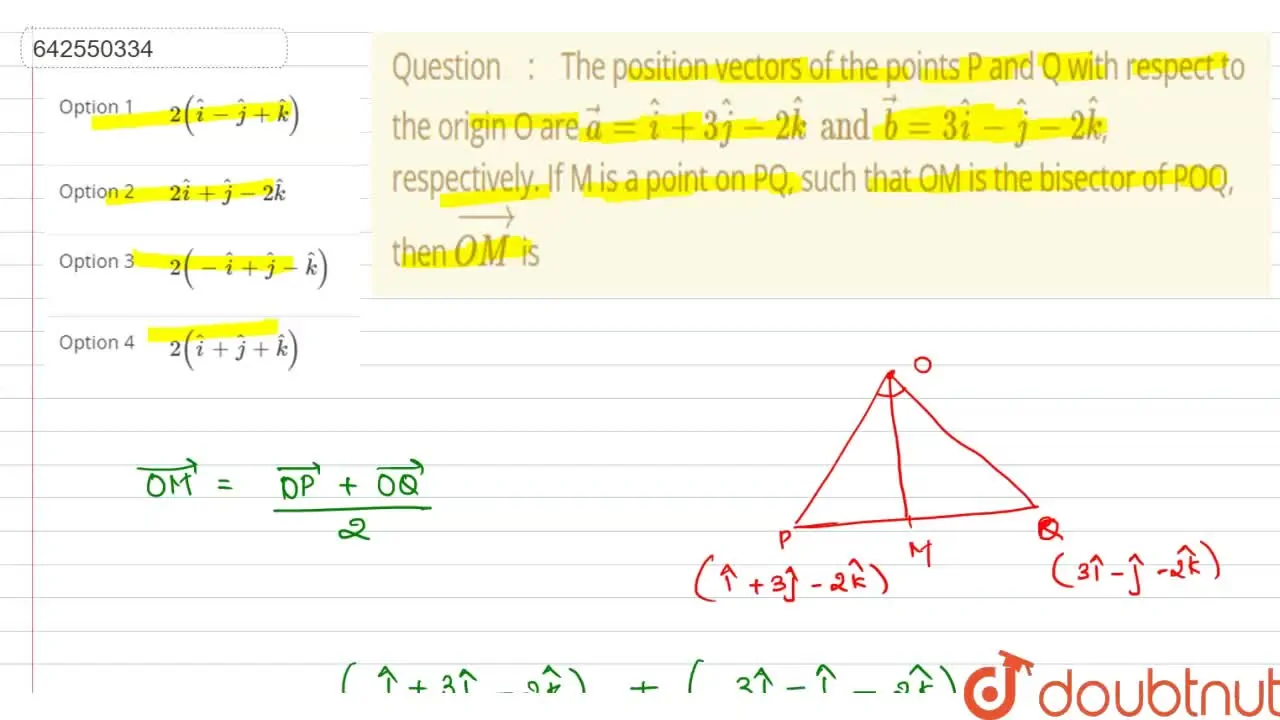
The position vectors of the points P and Q with respect to the origin O are →a=ˆi+3ˆj−2ˆkand→b=3ˆi−ˆj−2ˆk, respectively. If M is a point on PQ, such that OM is the bisector of POQ, then −−→OM is
2(ˆi−ˆj+ˆk)
2ˆi+ˆj−2ˆk
2(−ˆi+ˆj−ˆk)
2(ˆi+ˆj+ˆk)
The correct Answer is:B
Since ∣∣∣−−→OP∣∣∣=∣∣∣−−→OQ∣∣∣=√14,ΔOPQ is isosceles.
Hence, the internal bisector OM is perpendicular to PQ and M is the midpoint of P and Q. Therefore,
−−→OM=12(−−→OP+−−→OQ)=2ˆi+ˆj−2ˆk

Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - MULTIPLE CORRECT ANSWER TYPE13videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - REASONING TYPE11videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - SUBJECTIVE14videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE ENGLISHCHAPTER - INTEGRALSEXERCISE - All Questions764videos
INTEGRALS
- BOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Archives (Numerical Value type)2videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
If →a=2ˆi−3ˆj−ˆk and →b=ˆi+4ˆj−2ˆk, then →a×→b is
View SolutionIf →a=2ˆi−3ˆj−1ˆkand→b=ˆi+4ˆj−2ˆk then →a×→b is
View SolutionThe position vectors of points A and B w.r.t. the origin are →a=ˆi+3ˆj−2ˆkand→b=3ˆi+ˆj−2ˆk, respectively. Determine vector −−→OP which bisects angle AOB, where P is a point on AB.
View Solutionfind →A×→B if →A=ˆi−2ˆj+4ˆkand→B=3ˆi−ˆj+2ˆk
View SolutionIf →a=3ˆi+ˆj−4ˆkand→b=6ˆi+5ˆj−2ˆk find ∣∣→aX→b∣∣
View SolutionThe position vectors of the points A, B, C are 2ˆi+ˆj−ˆk,3ˆi−2ˆj+ˆkandˆi+4ˆj−3ˆk respectively . These points
View SolutionThe position vectors of the points A, B, C are 2ˆi+ˆj−ˆk,3ˆi−2ˆj+ˆkandˆi+4ˆj−3ˆk respectively . These points
View SolutionThe position vectors of the points A, B, C are 2ˆi+ˆj−ˆk,3ˆi−2ˆj+ˆkandˆi+4ˆj−3ˆk respectively . These points
View SolutionFind ∣∣→a×→b∣∣, if →a=2ˆi−7ˆj+7ˆk and →b=3ˆi−2ˆj+2ˆk
View SolutionIf →a=4ˆi+3ˆj+2ˆkand→b=3ˆi+2ˆk , find ∣∣→b×2→a∣∣
View Solution