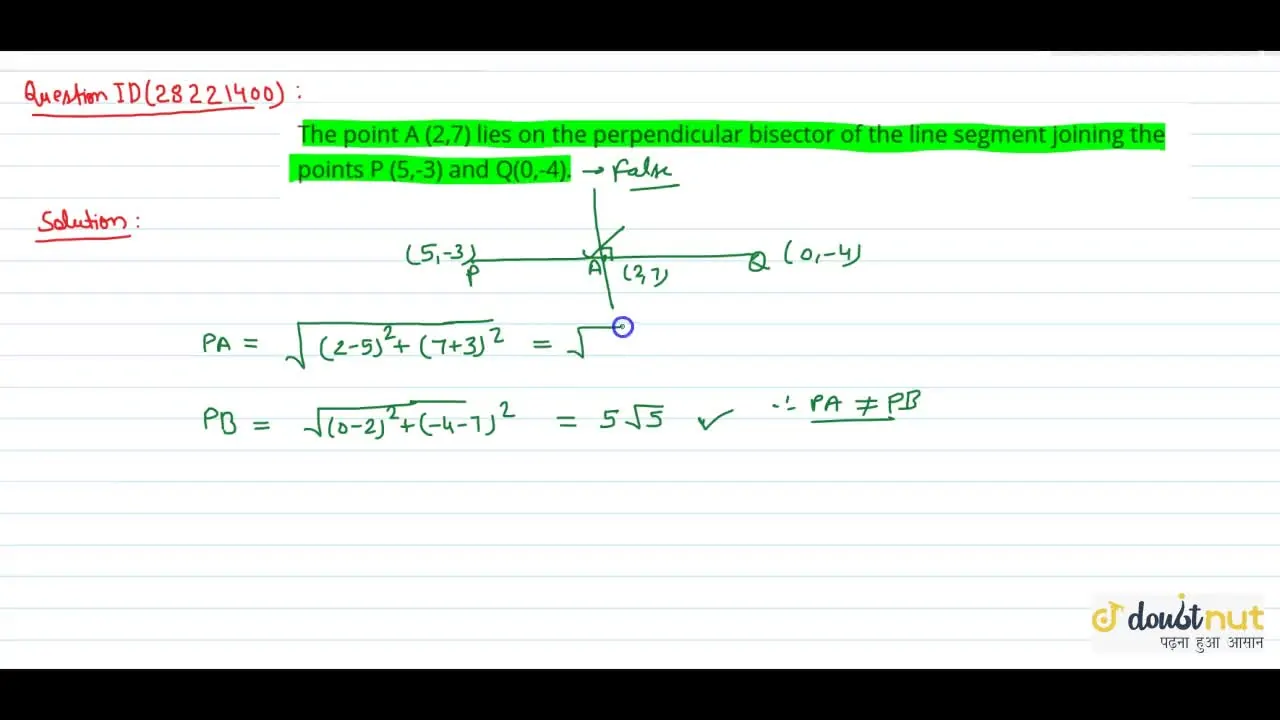
The point A (2,7) lies on the perpendicular bisector of the line segment joining the points P (5,-3) and Q(0,-4).
If A (2,7) lies on perpendicular bisector of P(6,5) and Q(0,-4) , then AP = AQ
AP
and A
So, A does not lies on the perpendicular bisector of PQ.
Alternate Method
If the point A(2,7) lies on the perpendicular bisector of the line segment , then the point A satisfy the equation of perpendicular bisector.
Now , we find the equation of equation of perpendicular bisector . For this , we find the slope perpendicular bisector.
Slope of perpendicular
[
[since, perpendicular bisector is perpendicular to the line segment , so its slopes have the condition ,
Since , the perpendicular bisector passes through the mid- point of the line segment joining the points (5,-3) and (0,4).
Mid - point of PQ
So , the equation of perpendicular bisector having slop and passes through the mid - point is
[equation of line is
...(i)
Now , check whether the point A(2,7) lie on the Eq. (i) or not.
Hence, the point A(2,7) does not lie on the perpendicular bisector of the line segment.
Related Playlists
- BOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
- BOOK - NCERT EXEMPLARCHAPTER - INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSEXERCISE - Introduction To Trigonometry And Its Applications60videos
INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONS
Similar Questions
The point which lies on the perpendicular bisector of the line sequent joining the points P(−2,0) and Q(2,5) is
View SolutionWhich point lies on the perpendicular bisector of the line segment joining the points A (-3, 4) andB (3,-4)?
View SolutionThe point which lies on the perpendicular bisector of the line segment joining the points A(-2,-5) and B (2,5) is
View SolutionFind the coordinates of the point Q on the X- axis which lies on the perpendicular bisector of the line segment joining the points A (-5,-2) and B (4,-2). Name the type of triangle formed by the points Q , A and B.
View SolutionThe coordinates of a point on x-axis which lies on the perpendicular bisector of the line segment joining the points (7, 6) and (−3, 4) are (0, 2) (b) (3, 0) (c) (0, 3) (d) (2, 0)
View SolutionFind the equation of the perpendicular bisector of the line segment joining the points (1,1) and (2,3).
View SolutionFind the equation of the perpendicular bisector of the line segment joining points (7,1) and (3,5).
View SolutionFind the equation of the perpendicular bisector of the line segment joining the points (1,0) and (3,5).
View SolutionFind the equation of the perpendicular bisector of the line segment joining the points A(2,3)andB(6,−5).
View SolutionFind the equation of the perpendicular bisector of the line segment joining the points A(2,3) and B(6,−5).
View Solution