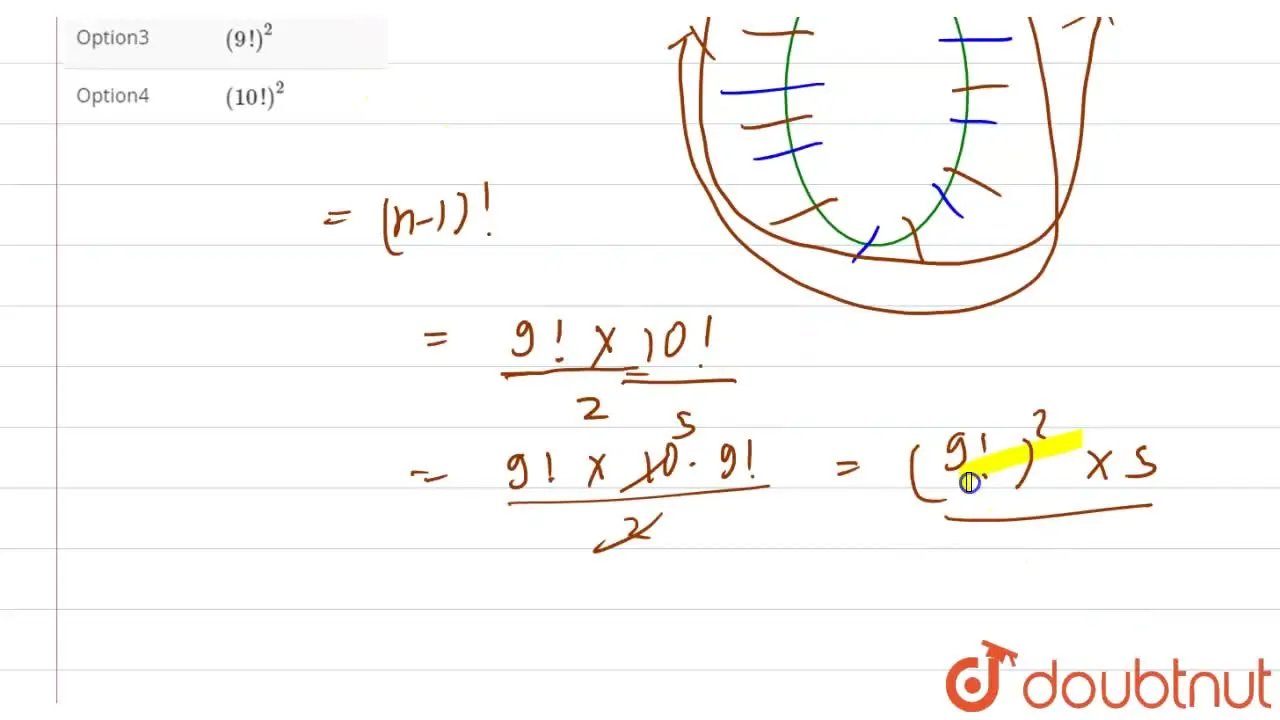
The number of ways in which 20 different pearls of two colours can be set alternately on a necklace, there being 10 pearls of each colour, is
9!×10!
5(9!)2
(9!)2
(10!)2
The correct Answer is:B
Step by step video & image solution for The number of ways in which 20 different pearls of two colours can be set alternately on a necklace, there being 10 pearls of each colour, is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - PERMUTATION & COMBINATIONEXERCISE - LEVEL-288videos
PERMUTATION & COMBINATION
- BOOK - VMC MODULES ENGLISHCHAPTER - PERMUTATION & COMBINATIONEXERCISE - JEE ARCHIVE50videos
PERMUTATION & COMBINATION
- BOOK - VMC MODULES ENGLISHCHAPTER - PERMUTATION & COMBINATIONEXERCISE - JEE ARCHIVE50videos
PERMUTATION & COMBINATION
- BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 9EXERCISE - MATHEMATICS (SECTION 2)5videos
MOCK TEST 9
- BOOK - VMC MODULES ENGLISHCHAPTER - PROBABILITYEXERCISE - JEE ADVANCED (ARCHIVE)102videos
PROBABILITY
Similar Questions
The number of ways in which 5 beads of different colours can be made into a necklace is
View SolutionFind the number of ways in which 10 different diamonds can be arranged to make a necklace.
View SolutionFind the number of ways in which 12 different beads can be arranged to form a necklace.
View SolutionNumber of ways in which 12 different things can be distributed in 3 groups, is
View SolutionFind the number of ways in which (i) n different beads (ii) 10 differenet beads can be arranged to form a necklace.
View SolutionThe total number of ways in which 5 balls of different colours can be distributed among 3 persons so that each person gets at least one ball is
View SolutionThe total number of ways in which 5 balls of differert colours can be distributed among 3 persons so thai each person gets at least one ball is
View SolutionThe number of ways four boys can be seated around a round talble in four chairs of ditterent colours, is
View SolutionThe number of ways in which three girls and ten boys can be seated in two vans, each having numbered seats, three in the front and four at the back is
View SolutionThere are seven even greeting cards each of a different colour and seven envelopes of the same seven colours. Find the number of ways in which the cards can be put in the envelopes so that exactly four of the cards go into the envelopes of the right colour.
View Solution