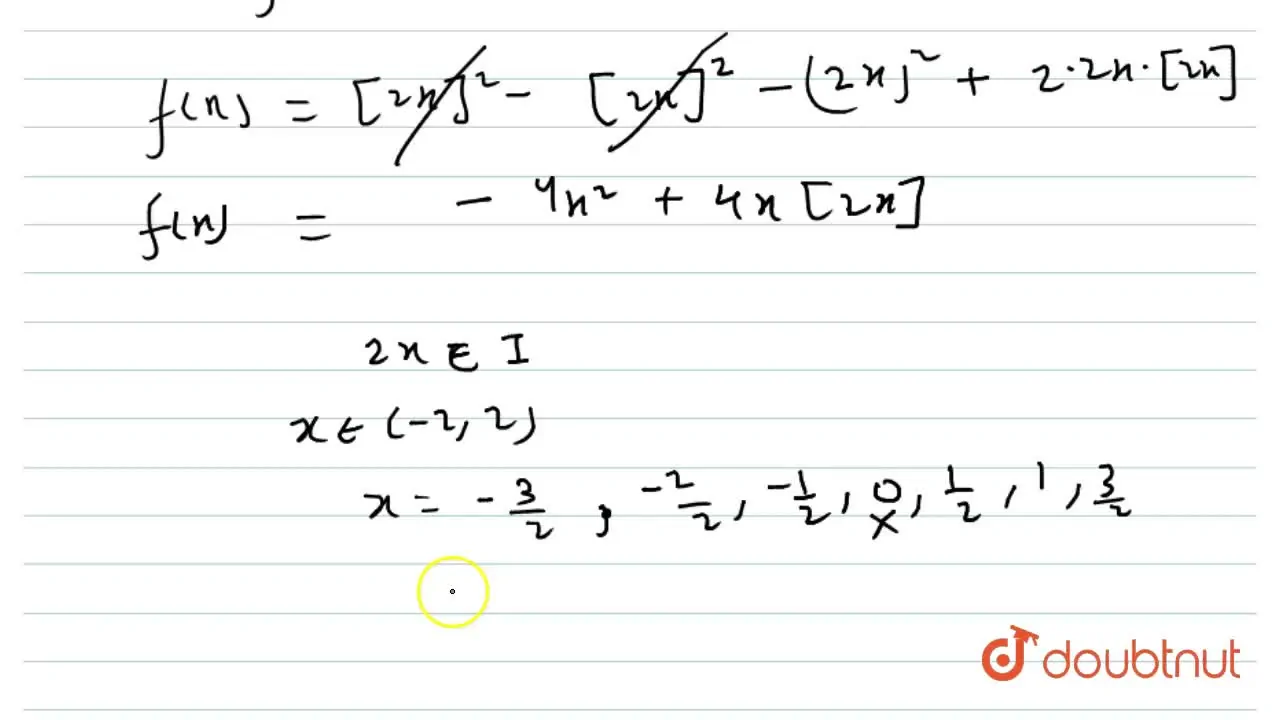The number of points of discontinuity of f(x)=[2x]2−{2x}2 (where [ ] denotes the greatest integer function and { } is fractional part of x) in the interval (−2,2), is
1
6
2
5
The correct Answer is:B
Given, f(x)=([2x]+{2x})([2x]−{2x})=4x−4x{2x}
2x∈(−4,4)
Hence f(x) is discontinuous when 2x=−3,−2,−1,1,2,3.
At x=0,f(x) is continuous
Related Playlists
- BOOK - CENGAGECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Multiple Correct Answer Type9videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - CENGAGECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Comprehension Type2videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises91videos
CONIC SECTIONS
- BOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
Similar Questions
The function f(x)=[x2]+[−x]2, where [.] denotes the greatest integer function, is
View SolutionIf f(x)=[2x], where [.] denotes the greatest integer function, then
View SolutionNumber of points of discontinuity of f(x)=[X2+1) in [−2,2] is equal to[Note : [x] denotes greatest integer function]
View Solutionf(x)=[x2]−{x}2, where [.] and {.} denote the greatest integer function and the fractional part function , respectively , is
View SolutionNumber of points of discontinuity of f(x)={x5}+{x2} in x∈[0,100] is/are (where [-] denotes greatest integer function and {:} denotes fractional part function)
View Solutionf(x)=sin−1[log2(x22)] where [ . ] denotes the greatest integer function.
View SolutionSolve 1x+1[2x]={x}+13where [.] denotes the greatest integers function and{.} denotes fractional part function.
View SolutionNumber of points of discontinuity of f(x)=[x3+3x2+7x+2], where [.] represents the greatest integer function in [0,1] is ___________.
View SolutionNumber of points of discontinuity of the function f(x)=[6xπ]cos[3xπ] where [y] denotes the greatest integer function less than or equal to y) in the interval [0,π2] is
View SolutionThe sum of solutions of the equation 2[x]+x=6{x} is (where [.] denotes the greatest integer function and {.} denotes fractional part function)
View Solution