The normal to the curve x2=4y passing (1,2) is
(A) x+y=3
(B) xy=3
(C) x+y=1
(D) xy=1
Option A is the correct answer
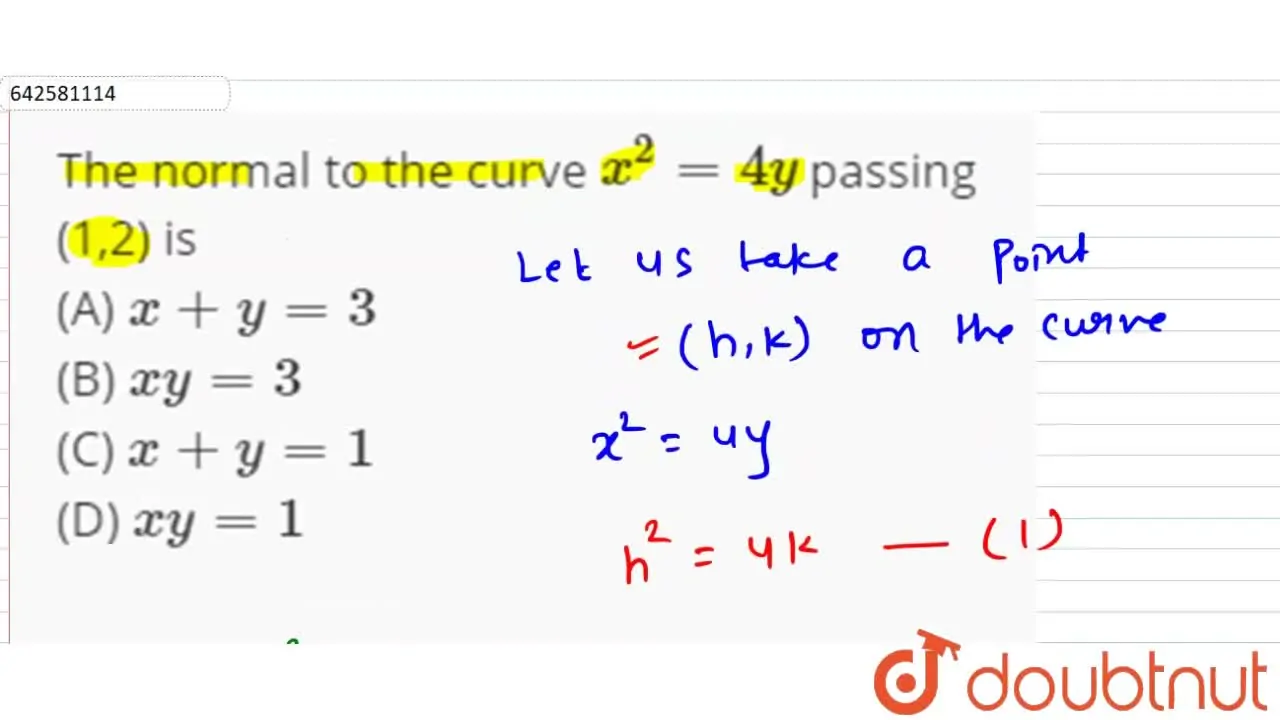
Given x2=4y
Slope of tangent to the curve will be 4dydx=2x
⇒dydx=x2
so, slope of normal will be −dxdy=−2x
Let the point on the curve be (h,k)
so slope of normal will be −2h
Equation of normal is given by (y−k)=−2h(x−h)
It is given that the normal passes through (1,2)
⇒(2−k)=−2h(1−h)..........(1)
Also, (h,k) lies on the curve so h2=4k
from (1) we have
h34=2h+2−2h=2
⇒h3=8
⇒h=2
⇒k=h24⇒k=1
so the equation will be
y−1=−22(x−2)
x+y=3
Related Playlists
- BOOK - NCERT ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.49videos
APPLICATION OF DERIVATIVES
- BOOK - NCERT ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - EXERCISE 6.529videos
APPLICATION OF DERIVATIVES
- BOOK - NCERT ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - EXERCISE 8.27videos
APPLICATION OF INTEGRALS
Similar Questions
The normal at the point (1,1) on the curve 2y+x2=3is
(A) x−y=0
(B) xy=0
(C) x+y+1=0
(D) xy=0View SolutionThe normal at the point (1,1) on the curve 2y+x2=3is
(A) x+y=0
(B) xy=0
(C) x+y+1=0
(D) xy=0View SolutionThe normal to the parabola y2=−4ax from the point (5a,2a) are (A) y=x−3a (B) y=−2x+12a (C) y=−3x+33a (D) y=x+3a
View SolutionThe following line(s) is (are) tangent to the curve y=x2−x (A) x−y=0 (B) x+y=0 (C) x−y=1 (D) x+y=1
View SolutionA tangent drawn to the curve y=f(x) at P(x,y) cuts the x-axis and y-axis at A and B respectively such that BP:AP=2:1. Given that f(1)=1. Answer the question:Equation of normal to curve at (1,1) is (A) x−4y+3=0 (B) x−3y+2=0 (C) x−2y+1=0 (D) none of these
View SolutionThe lines parallel to the normal to the curve xy=1 is/are (a)3x+4y+5=0 (b) 3x−4y+5=0 (c)4x+3y+5=0 (d) 3y−4x+5=0
View SolutionThe locus of the centre of the circle passing through (1,1) and cutting x2+y2=4 orthogonally is : (A) x+y=3 (B) x+2y=3 (C) 2x+y=3 (D) 2x−y=3
View SolutionArea bounded by the curves y=x and y=x3 is (A) 12 (B) 1 (C) 32 (D) 2
View SolutionLet (2,3) be the focus of a parabola and x+y=0 and x−y=0 be its two tangents. Then equation of its directrix will be (a) 2x−3y=0 (b) 3x+4y=0 (c) x+y=5 (d) 12x−5y+1=0
View SolutionArea common to the curves y=√x and x=√y is (A) 1 (B) 23 (C) 13 (D) none of these
View Solution