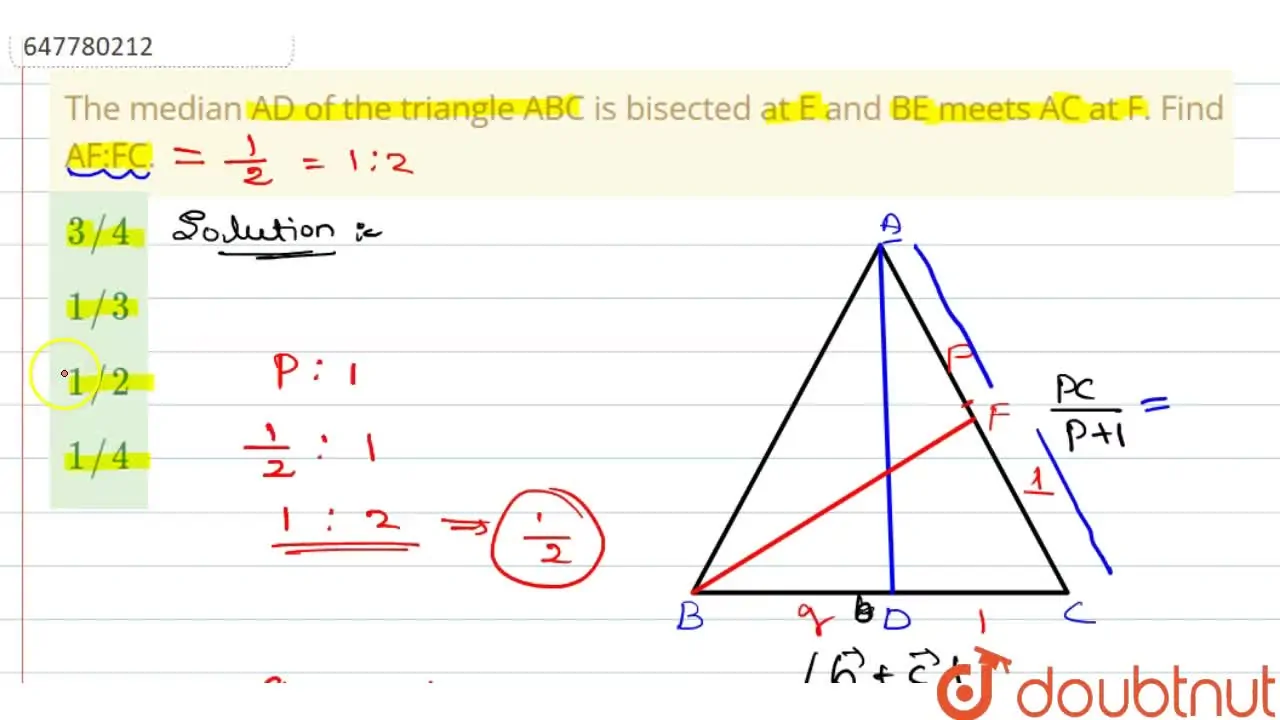
The median AD of the triangle ABC is bisected at E and BE meets AC at F. Find AF:FC.Solution in Kannada
3/4
1/3
1/2
1/4
The correct Answer is:B
Let position vector of A w.r.t. B is a and that of C w.r.t. B is c.

Position vector fo D w.r.t.
B=0+c2=c2
Position vector of
E=a+c22=a2+c4 . . . (i)
Let AF:FC=λ:1andBE:EF=μ:1
Position vector of F=λc+a1+λ
Now, position vector of
E=μ(λc+a1+λ)+1⋅0μ+1 . . . (ii)
From eqs. (i) and (ii), we get
a2+c4=μ(1+λ)(1+μ)a+λu(1+λ)(1+μ)c
⇒12=μ(1+λ)(1+μ)
and 14=λμ(1+λ)(1+μ)
⇒λ=12
∴AFAC=AFAF+FC=λ1+λ=1232=13.
Similar Questions
In ΔABC, AD is a median and E is the midpoint of AD. BE is extended to intersect AC at F. Prove that AF=13AC.
03:47View SolutionThe median AD to ΔABC is bisected at E and BE is produced to meet the side AC in F. Show that ¯¯¯¯¯¯AF=13¯¯¯¯¯¯AC
03:37View SolutionThe median AD of the triangle ABC is bisected at E. BE meets AC in F then AF : AC is
08:55View SolutionΔABC में, AD एक माध्यिका है । ∠ADB और ∠ADC के समद्विभाजक क्रमशः AB एवं AC से E एवं F बिन्दु पर मिलते है । सिद्ध कीजिए कि EF∣∣BC है ।
07:04View Solutionएक त्रिभुज ABC में, AD एक मध्यिका है। ∠ADB और ∠ADC के कोण अर्द्धक AB और AC को क्रमश: E व F पर मिलते है। AE:BE=3:4,EF:BC=?
View SolutionIn a ΔABC,AD is a median. The bisectors of ∠ADBand∠ADC meets AB & AC at E and F respectively . AE:BE=3:4 . Find EF:BC.
06:52View SolutionIn a triangle ABC, AD is a medium and E is mid-point of median AD. A line through B and E meets AC at point F.
03:09View SolutionInΔABC,AD is the bisector of∠A meeting BC at D, CF⊥AB and E is the mid-point of AC. Then median of the triangle is
03:07View Solution