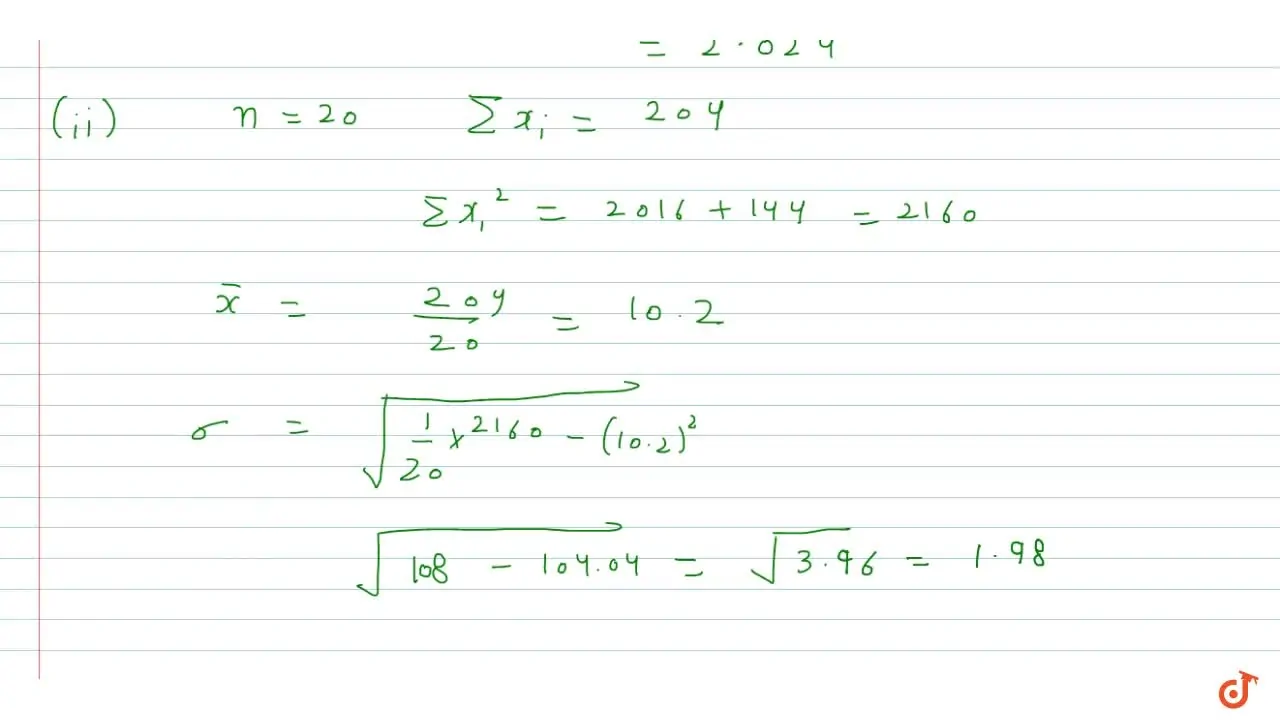The mean and standard deviation of 20 observations are found to be 10 and 2, respectively. One rechecking, it was found that an observation 8 was incorrect. Calculate the correct mean and standard deviation in each of the following cases. (i) If wrong item is omitted (ii) If it is replaced by 12.
¯x=∑xin=10=∑xi20
∑xi=200
for 19 terms =200−8=192=∑xi
σ=√1n⋅∑x2i−(¯x)2
let incorrect sum be e∑
2=√1n⋅e∑x2i−100
4=120e∑x2i−100
e∑x2i=104⋅20=2080
correct ∑x2i for 19 terms = 2080−64=2016
(i)¯x=19219=10.1
σ=√119⋅2016−(10.1)2
=√106.1−102=√4.1=2.024
(ii) n = 20 ∑xi=204
∑x2i=2016+144=2160
¯x=20420=10.2
σ=√120⋅2160−(10.2)2
=√108−104.04=√3.96=1.98
Related Playlists
Similar Questions
The mean and standard deviation of 18 observations are found to be 7 and 4 respectively. On rechecking it was found that an observation 12 was misread as 21. Calculate the correct mean and standard deviation.
View SolutionThe mean and standard deviation of 20 observations are found to be 10 and 2, respectively. On review, it was found that an observation 8 was incorrect. Then the correct standard deviation if the wrong item is omitted is …………..
View SolutionThe mean and standard deviation of 20 observations are found to be 10 and 2 respectively. On rechecking, it was found that an observation 8 was incorrect. Find the new standard deviation if wrong item is omitted.
View SolutionThe mean and variance of 10 observation are found to be 10 and 4 respectively. On rechecking it was found that an observation 8 was incorrect. If it is replaced by 18, then the correct variance is
View SolutionThe mean and standard deviation of 20 observations are found to be 10 and 2 . On rechecking , it was found that an observation 8 was incorrect. Find the correct standard deviation if wrong item is omitted .
View SolutionThe mean and variance of 20 observations are found to be 10 and 4. respectively. On rechecking, it was found that an observation 9 was incorrect and the correct observation was 11. Then the correct variance is
View SolutionThe mean and variance of 20 observations are found to be 10 and 4 respectively. On rechecking, it was found that an observation 8 is incorrect. If the wrong observation is omitted, then the correct variance is
View SolutionThe mean and variance of 10 observations are found to be 10 and 5 respectively. On rechecking it is found that an observation 5 is incorrect. If the incorrect observation is replaced by 15, then the correct variance is
View SolutionThe mean and standard deviation of 100 observations were calculated as 40 and 5.1, respectively by a student who took by mistake 50 instead of 40 for one observation. What are the correct mean and standard deviation?
View SolutionThe mean and standard deviation of 100 observations were calculated as 40 and 5.1 respectively by a student who took by mistake 50 instead of 40 for one observation. What are the correct mean and standard deviation?
View Solution