The maximum volume (in cu.m) of the right circular cone having slant height 3 m is
43π
2√3π
3√3π
6π
The correct Answer is:B
Let h= height of the cone,
r= radius of circular base ltbr =√(3)2−h2 [∴L2=h2+r2]
=√9−h2 ...(i)
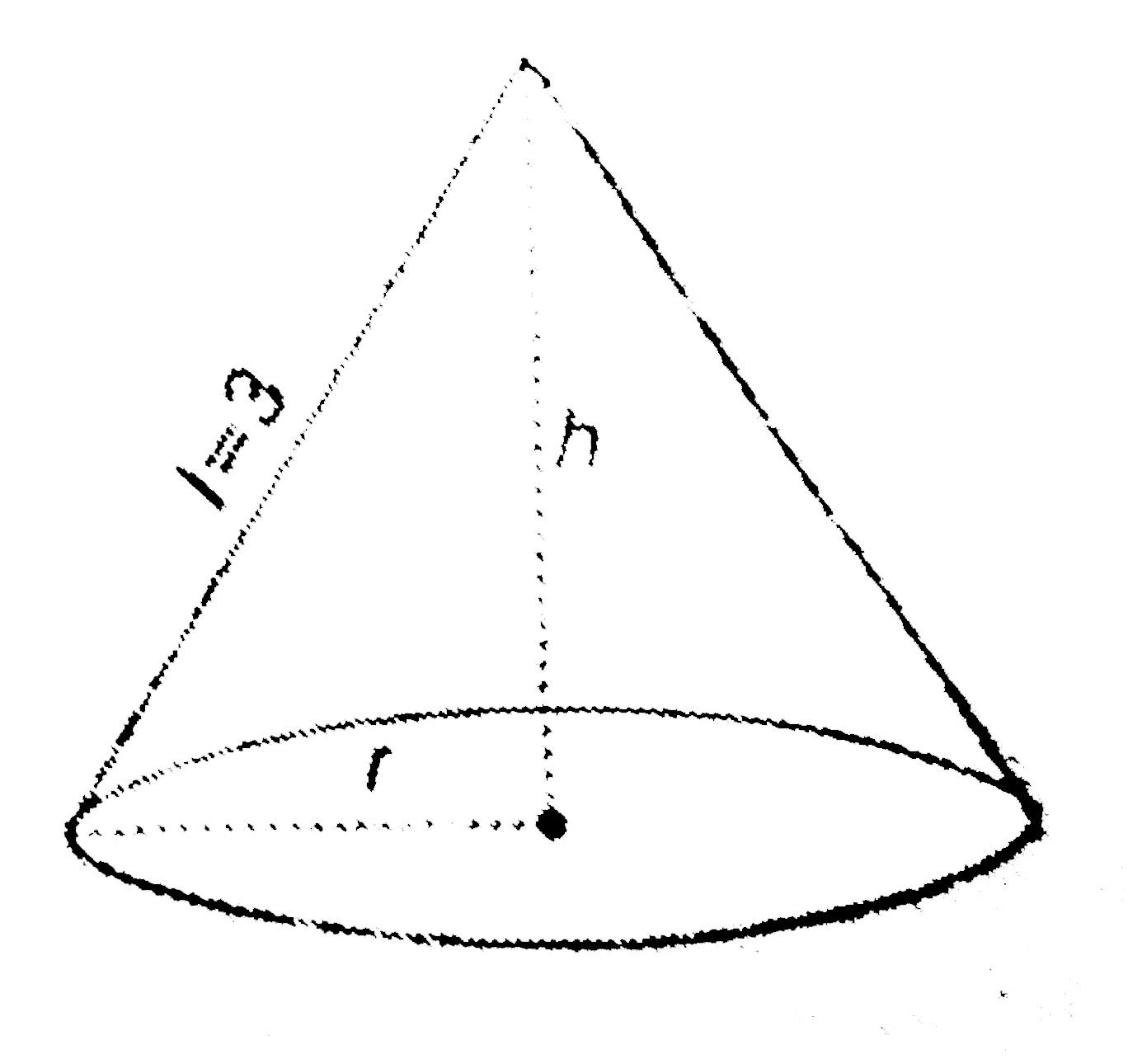
Now, volume (V) of cone =13πrr2h
⇒V(h)=13π(9−h2)h [ From Eq. (ii)]
=13π[9h−h2] ...(ii)
For maximum volumne V'(h)=0andV''(h)≤0
Here V'(h)=0⇒(9−3h2)=0
rArr h=sqrt(3)" " [ :. h cancellt]
and V''(h)=13π(−6h)≤0forh=√3
Thus, volume is maximum when h=√3
Now, maximum volume
V(√3=13π(9√3−3√3) [ From Eq. (iii)]
=2√3π
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA (OBJECTIVE QUESTIONS II)8videos
APPLICATION OF DERIVATIVES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - MAXIMA AND MINIMA (MATCH THE COLUMNS)1videos
APPLICATION OF DERIVATIVES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - ROLLES AND LAGRANGES THEOREM (ANALYTICAL & DESCRIPTIVE QUESTION)1videos
APPLICATION OF DERIVATIVES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - 3D GeometryEXERCISE - Equation of Plane Objective Question II (Integer Answer Type Question)1videos
3D Geometry
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - AREAEXERCISE - AREA USING INTEGRATION55videos
AREA
Similar Questions
The maximum volume (in cu.m) of the right circular cone having slant height 3m is k√3π . The value of k is ________.
View SolutionVolume of frustum of right circular cone
View SolutionVolume of a Right Circular Cone
View SolutionThe volume of a right circular cone of height 3 cm and slant height 5 cm is
View SolutionIf the ratio of the radius of the base of a right circular cone to its slant height is 1 : 3, what is the ratio of the total surface area to the curved surface area ?
View SolutionFind the surface area of a frustum of a right circular cone with a slant height of 30 m, lower base radius 20 m and top radius of 15 m ?
View SolutionThe radius of the base of a right circular cone is 6 cm and its slant height is 10 cm. Then its volume is (Use π=227)
View SolutionThe total surface area of a right circular cone of slant height 13 cm is 90πcm2 , find its radius and volume.
View SolutionThe diameter of the base of a right circular cone is 18 cm and its slant height is 15cm. Find the height of the cone.
View SolutionFind the total surface area (in cm2) of a right circular cone of diameter 21 cm and slant height 11 cm.
View Solution


