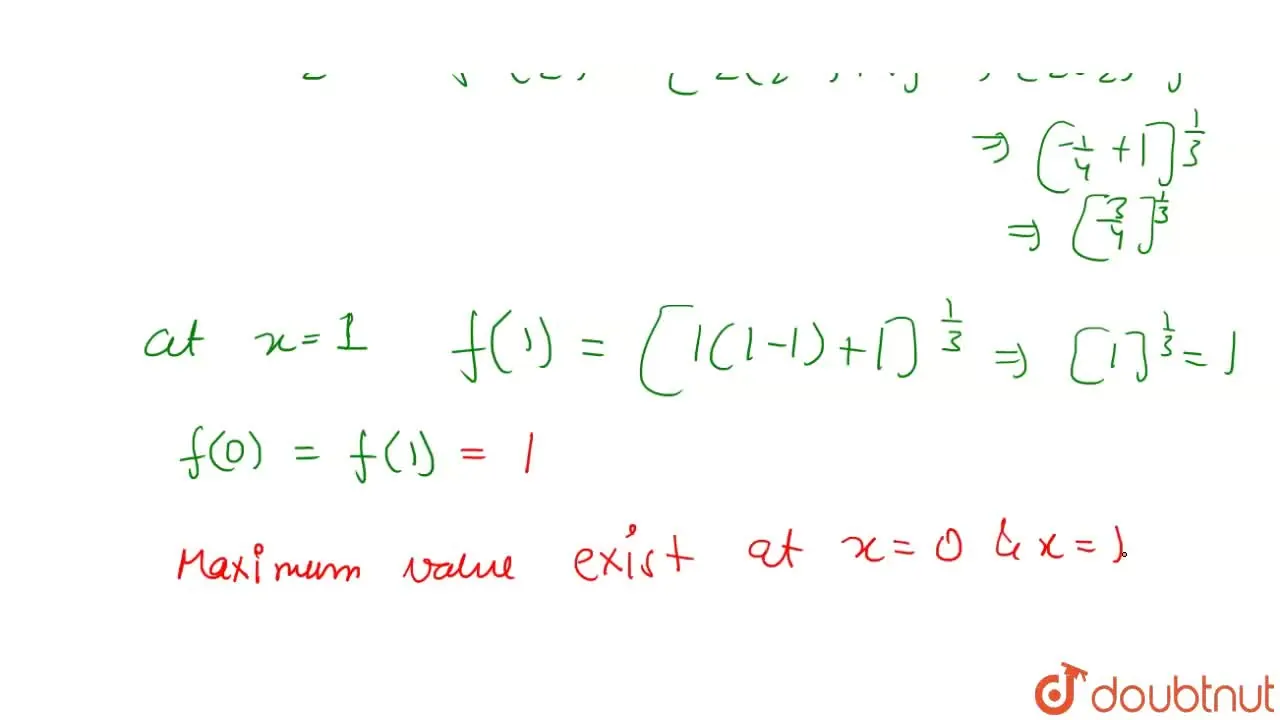The maximum value of [x(x−1)+1]13,0≤x≤1is(A) (13)13 (B) 12 (C) 1 (D) 0
f(x)=[x(x−1)+1]13
⇒f(x)=[x2−x+1]13
If we differentiate x2−2x+1 w.r.t. x, we get 2x−1.
It means, the given function is decreasing from 0 to 12 and then it is increasing from 12 to 1.
So, maximum value of f(x) will be on bounadries.
∴f(0)=f(1)=1
So, option (c) is the correct option.
Similar Questions
The maximum value of [x(x−1)+1]13,0≤x≤1 is:
View SolutionWhat is the minimum value of [x(x−1)+1]13 where 0<x<1 ?
View SolutionThe maximum value of the function f(x)=[x(x−1)+1]13; x in [0,1] is
View SolutionIf α+β=900 ,then the minimum and maximum values of cosα⋅cosβ are
(A) −13 and 13
(B) −1 and 1
(C) −14 and 14
(D) −12 and 12View SolutionThe maximum value of the function f(x)=(1+x)0.31+x0.3 in [0,1] is
View SolutionIf x2+3x+3=0 and ax2+bx+1=0 ,a,b in Q have a common root,then value of (3a +b) is equal to : (A) 13 (B) 1 (C) 2 (D) 4
View SolutionThe greatest value of f(x)=(x+1)1/3−(x−1)1/3 on [0, 1] is
(a) 1
(b) 2
(c) 3
(d) 13View SolutionFor all real values of x, the minimum value of 1−x+x21+x+x2 is
(A) 0
(B) 1
(C) 3
(D) 13View SolutionIf X2+4x+3=0, then the value of X3X6+27x3+27 is (A) -1 (B) −12 (C) 1 (D) 1/2
View SolutionValue of [(13)−1−(14)−1]−1
( a ) 1
( b ) 0
( c ) 3
( d ) -1View Solution