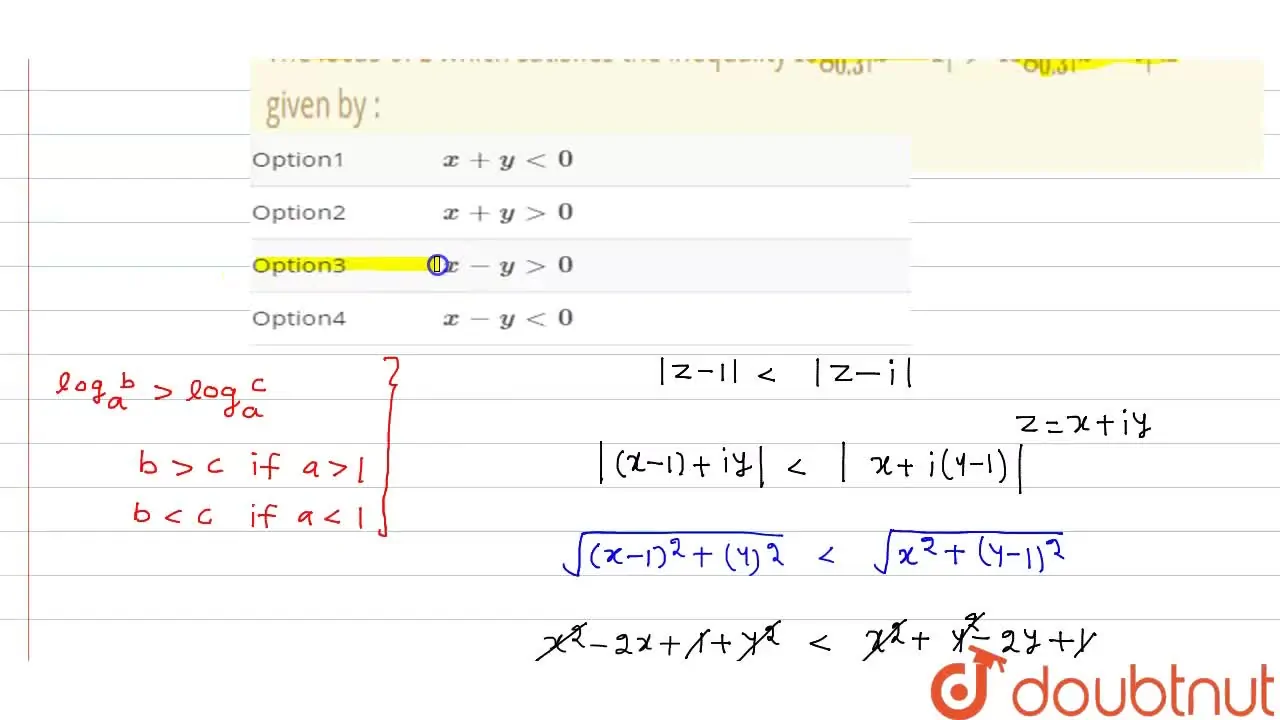
The locus of z which satisfies the inequality log0.3|z−1|>log0.3|z−i| is given by :
x+y<0
x+y>0
x−y>0
x−y<0
The correct Answer is:C
Step by step video & image solution for The locus of z which satisfies the inequality log _(0.3) abs(z-1) gt log _(0.3) abs(z-i) is given by : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - LEVEL - 250videos
COMPLEX NUMBERS
- BOOK - VMC MODULES ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - NUMRICAL VALUE TYPE FOR JEE MAIN14videos
COMPLEX NUMBERS
- BOOK - VMC MODULES ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - JEE ARCHIVE76videos
COMPLEX NUMBERS
- BOOK - VMC MODULES ENGLISHCHAPTER - CIRCLESEXERCISE - JEE ADVANCED ( ARCHIVE )68videos
CIRCLES
- BOOK - VMC MODULES ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - JEE ADVANCED ARCHIVE76videos
CONIC SECTIONS
Similar Questions
The locus of point z satisfying Re(z2)=0, is
View Solutionlocus of the point z satisfying the equation |z−1|+|z−i|=2 is
View SolutionLet C1andC2 are concentric circles of radius 1and83 respectively having centre at (3,0) on the argand plane. If the complex number z satisfies the inequality log13(|z−3|2+211|z−3|−2)>1, then (a) z lies outside C1 but inside C2 (b) z line inside of both C1 and C2 (c) z line outside both C1 and C2 (d) none of these
View SolutionNumber of integers satisfying the inequality (log)12|x−3|≻1 is.....
View SolutionThe locus of the points z satisfying the condition arg (z−1z+1)=π3 is, a
View SolutionThe locus of the complex number z satisfying the inequaliyt log1√2(|z−1|+62|z−1|−1)>1(2where|z−1|≠12) is (A) a circle (B) interior of a circle (C) exterior of circle (D) none of these
View Solutionstatement-1 Locus of z satisfying the equation |z−1|+|z−8|=5 is an ellipse.
statement-2 Sum of focal distances of any point on ellipse is constant for an ellipse.View SolutionIf z is a complex number which simultaneously satisfies the equations
3|z−12|=5|z−8i| and |z−4|=|z−8|, where i=√−1, then Im(z) can beView SolutionIf log13|z+1|>log13|z−1| then prove that Re(z) < 0.
View SolutionFind the locus of z satisfying ∣∣∣z−3z+1∣∣∣=3 in the complex plane.
View Solution