Find the locus of the foot of the perpendicular drawn from the center upon any tangent to the ellipse x2a2+y2b2=1.
(x2−y2)2=a2x2+b2y2
(x2−y2)2=a2x2−b2y2
(x2+y2)2=a2x2+b2y2
(x2+b2)2=a2x2−b2y2
The correct Answer is:C
Let P (h, k) be the foot of the perpendicular drawn from the centre C (0, 0) of the ellipse to any tangent
y=mx+√a2m2+b2 …(i)
Then, k=mh+√a2m2+b2⇒(k−mh)2=a2m2+b2 …(ii)
Since CP is perpendicular to the tangent given in (i).
∴kh×m=−1⇒m=−hk
Substituting the value of m in (ii), we get
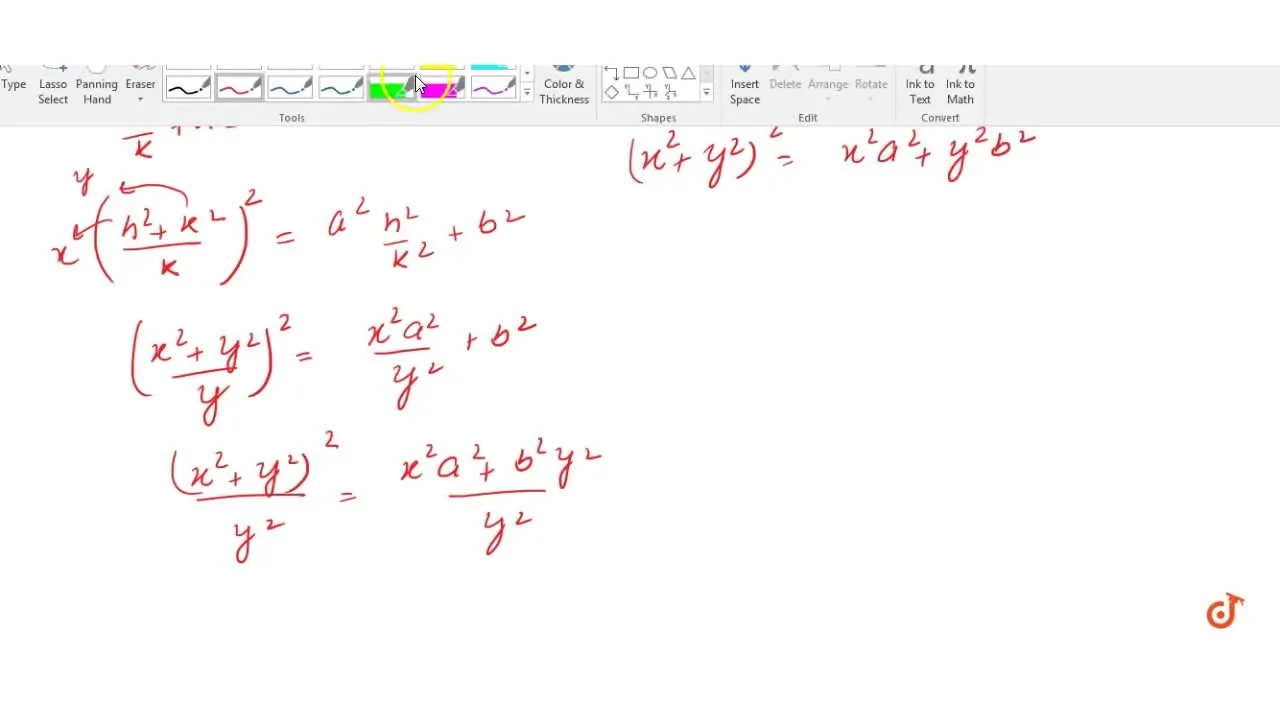
(h2+k2)2=a2h2+b2k2
Hence, the locus of P (h, k) is a2x2+b2y2=(x2+y2)2
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - ELLIPSEEXERCISE - Section II - Assertion Reason Type7videos
ELLIPSE
- BOOK - OBJECTIVE RD SHARMACHAPTER - ELLIPSEEXERCISE - Exercise82videos
ELLIPSE
- BOOK - OBJECTIVE RD SHARMACHAPTER - ELLIPSEEXERCISE - Chapter Test30videos
ELLIPSE
- BOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIATIONEXERCISE - Chapter Test30videos
DIFFERENTIATION
- BOOK - OBJECTIVE RD SHARMACHAPTER - EXPONENTIAL AND LOGARITHMIC SERIESEXERCISE - Chapter Test20videos
EXPONENTIAL AND LOGARITHMIC SERIES
Similar Questions
The locus of the foot of the perpendicular drawn from the centre upon any tangent to the ellipse x2a2+y2b2=1, is
View SolutionThe locus of the foot of the perpendicular drawn from the centre on any tangent to the ellipse x225+y216=1 is:
View SolutionThe product of the perpendicular drawn from the foci upon any tangent to any ellipse
View SolutionThe product of the perpendicular drawn from the foci upon any tangent to any ellipse
View SolutionIf the locus of the foot of the perpendicular drawn from centre upon any tangent to the ellipse x240+y210=1 is (x2+y2)2=ax2+by2, then (a−b) is equal to
View SolutionThe locus of the foot of the perpendicular from the foci an any tangent to the ellipse x2a2+y2b2=1, is
View SolutionFind the locus of the foot of the perpendicular drawn from a fixed point to any tangent to a parabola.
View SolutionThe locus of the foot of the perpendicular drawn from the origin to any tangent to the hyperbola x236−y216=1 is
View SolutionProduct of perpendiculars drawn from the foci upon any tangent to the ellipse 3x2+4y2=12 is
View SolutionFind the locus of the foot of perpendicular from the centre upon any normal to line hyperbola x2a2−y2b2=1.
View Solution