The locus of the centres of circles which touches (y−1)2+x2=1 externally and also touches X-axis is
{x2=4y,y≥0}∪{0,y),y<}
x2=y
y=4x2
y2=4x∪(0,y),y∈R
The correct Answer is:A
Let the locus of centre of circle be (h, k) touching (y−1)2+x2=1 = 1 and X-axis shown as
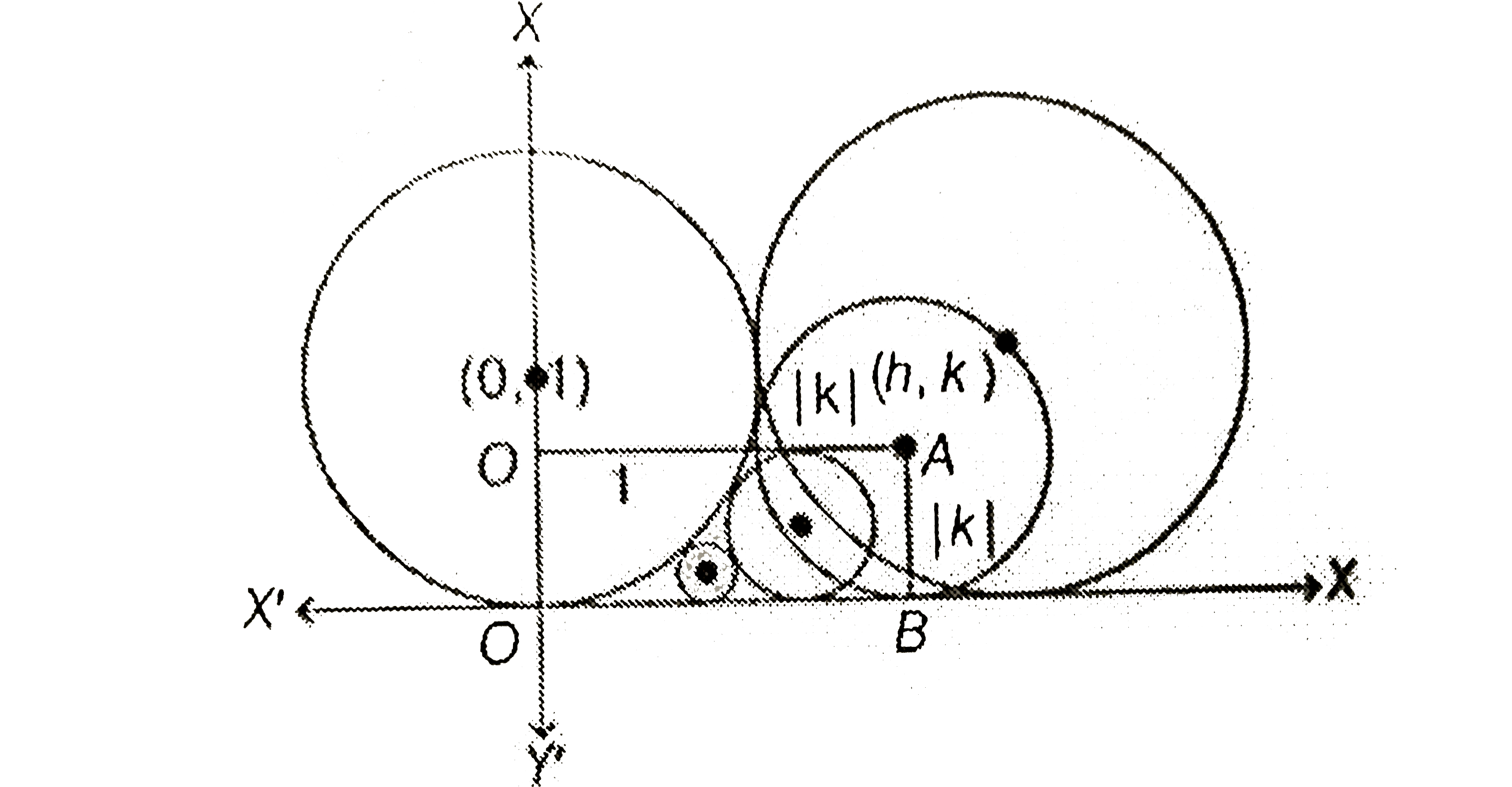
Clearly, from figure,
Distance between C and A is always 1 + |k|,
i.e. √(h−0)2+(k−1)2=1+|k|,
⇒h2+k2−2k+1=1+k2+2|k|
⇒h2=2|k|+2k⇒x2=2|y|+2y
where |y|={y , y≥0y , y<0
∴x2=2y+2y,y≥0
andx2=−2y+2y,y<0
⇒x2=4y, when y≥0
andx2=0, when y<0
∴{(x,y):x2=4y, when y≥0}∪{(0,y):y<0}
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 4 Fill in the blanks4videos
CIRCLE
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 4 Analytical & Descriptive Questions7videos
CIRCLE
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - CIRCLEEXERCISE - Topic 3 Integer Answer Type Question1videos
CIRCLE
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - BINOMIAL THEOREMEXERCISE - Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )8videos
BINOMIAL THEOREM
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - COMPLEX NUMBERSEXERCISE - TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)1videos
COMPLEX NUMBERS
Similar Questions
The locus of centre of the circle which touches the circle x2+(y−1)2=1 externally and also touches x-axis is
View SolutionThe locus of centre of the circle which touches the circle x2+(y−1)2=1 externally and also touches x-axis is
View SolutionThe locus of the centres of the circles which touch the circle x2+y2=1 externally also touch the y-axis and lie in the first quadrant, is
View SolutionThe locus of the centres of the circles, which touch the circle, x2+y2=1 externally, also touch the Y-axis and lie in the first quadrant, is
View SolutionLocus of centre of a circle which touches x2+y2−6x−6y+14=0 externally and also touches y-axis
View SolutionLocus of thews of the centre of the circle which touches x2+y2−6x−6y+14=0 externally and also y-axis is:
View SolutionThe locus of the centres of the circles which touch x2+y2=a2 and x^2+y^2=4ax, externally
View SolutionThe locus of the centre of a circle, which touches externally the circle x2+y2−6x−6y+14=0 and also touches the y-axis, is given by the equation
View SolutionThe locus of the centre of a circle, which touches externally the circle x2+y2−6x−6y+14=0 and also touches the y-axis, is given by the equation
View SolutionThe centres of those circles which touch the circle, x2+y2−8x−8y−4=0 , externally and also touch the x-axis, lie on : (1) a circle. (2) an ellipse which is not a circle. (3) a hyperbola. (4) a parabola.
View Solution


