The locus of the centre of a circle touching the circle x2+y2−4y−2x=2√3−1 internally and tangents on which from (1,2) is making a 60∘ angle with each other is a circle. then integral part of its radius is
(x−1)2+(y−2)2=3
(x−2)2+(y−1)2=1+2√3
x2+y2=1
none of these
The correct Answer is:D
Let C2(h,k)be the centre of the circle touching the given circle internally and r be its radius.
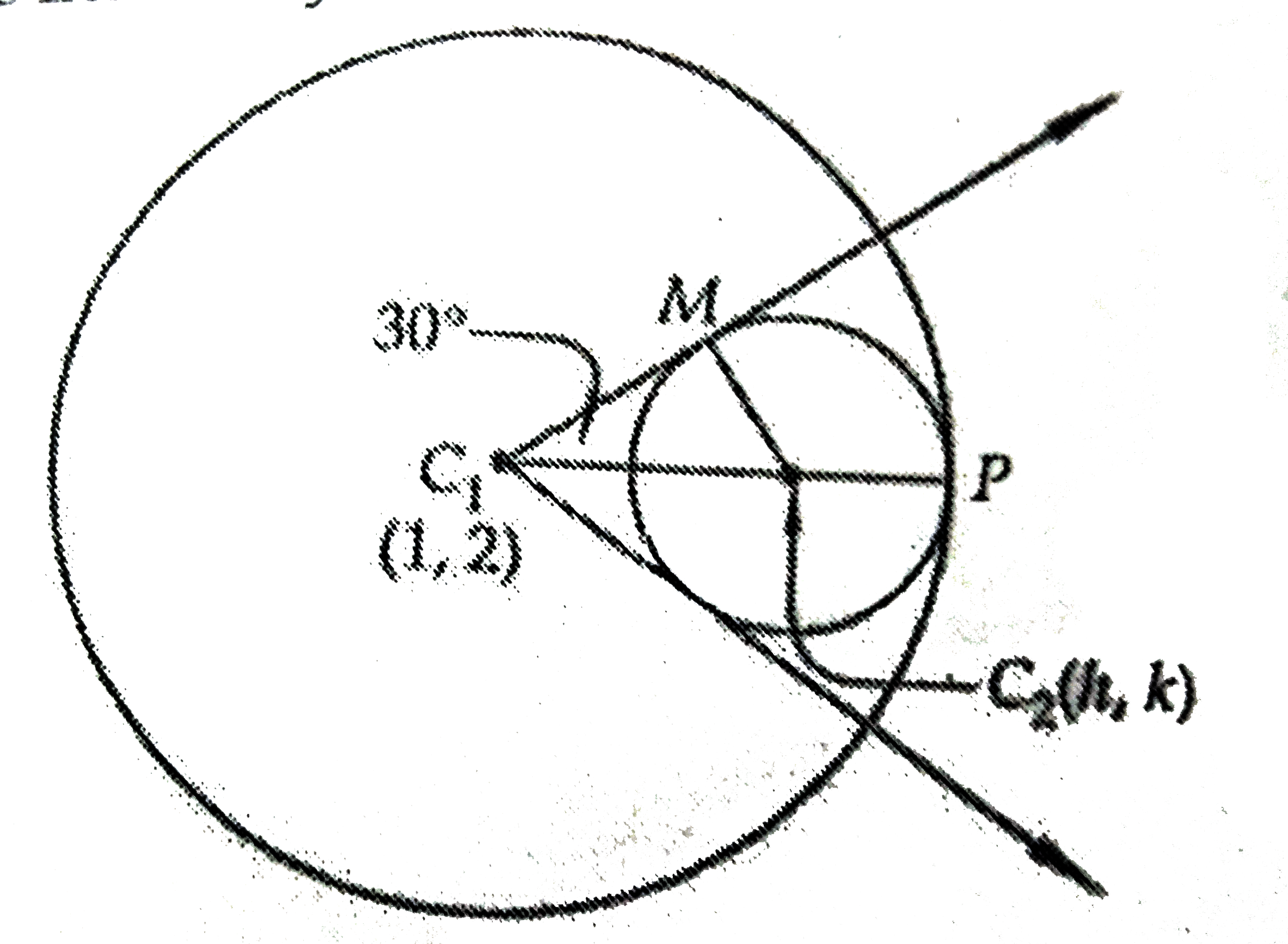
We have,
C1P=√1+4+2√3−1=√4+2√3
Since the circles touch each other internally.
∴C1C2=C1P−C2P
⇒√(h−1)2+(k−2)2=√4+2√3−r
⇒r=√4+2√3−√(h−1)2+(k−2)2
In ΔC1MC2, we have
sin30∘=C2MC1C2
⇒12=√4+2√3−√(h−1)2+(k−2)2√(h−1)2+(k−2)2
⇒3√(h−1)2+(k−2)2=2√4+2√3
⇒9[(h−1)2+(k−2)2]=4(4+2√3)
Hence, the locus of (h, k) is
9[(x−1)2+(y−2)2]=4(4+2√3)
Related Playlists
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)1videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section II - Assertion Reason Type12videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test53videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test30videos
CARTESIAN PRODUCT OF SETS AND RELATIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test58videos
COMPLEX NUMBERS
Similar Questions
Find the locus of the center of the circle touching the circle x2+y2−4y−2x=4 internally and tangents on which from (1, 2) are making of 600 with each other.
View SolutionFind the locus of the center of the circle touching the circle x2+y2−4y−2x=4 internally and tangents on which from (1, 2) are making of 600 with each other.
View SolutionFind the locus of the centre of the circle touching the line x+2y=0andx=2y
View SolutionFind the radius and centre of the circle of the circle x2+y2+2x+4y−1=0.
View SolutionThe locus of the centre of the circle cutting the circles x2+y2–2x−6y+1=0,x2+y2−4x−10y+5=0 orthogonally is
View SolutionThe locus of the centre of the circle which moves such that it touches the circle (x+1)2+y2=1 externally and also the y-axis is
View SolutionThe locus of centres of all circles which touch the line x = 2a and cut the circle x2+y2=a2 orthogonally is
View SolutionThe locus of the centres of the circles which touch x2+y2=a2 and x2+y2=4ax, externally
View SolutionThe locus of the centre of the circle passing through the intersection of the circles x2+y2=1 and x2+y2−2x+y=0 is
View SolutionThe locus of the centres of the circles which touch x2+y2=a2 and x^2+y^2=4ax, externally
View Solution


