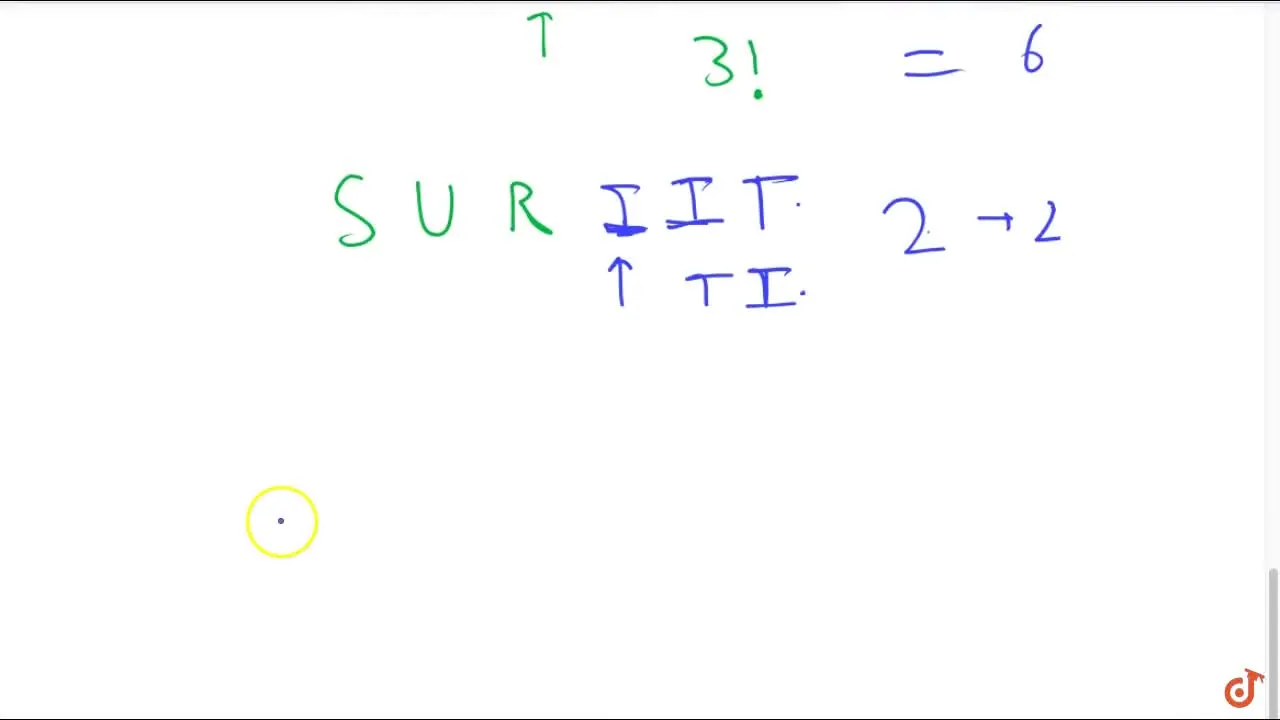The letters of the word SURITI are written in all possible orders and these words are written out as in a dictionary. Find the rank of the word SURITI.
In a dictionary the words at each stage are arranged in alphabetical order. We must consider the words beginning with I,R,S,T,U in order.
Number of words starting with I=5! =120
Number of words starting with
Number of words beginning with S is , but one of these words is the word SURITI, So, we first find the number of words beginning with SI,SR,ST
Number of words starting with
Number of words starting with SR=
Number of words starting with
Now, the words beginning with SU must follow. There are words beginning with SU, but one of these words is the word SURITI, Number of words starting with SUI=3!=6. The first word beginning with SUR is SURIIT and the next word is SURITI.
Rank of SURITI
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Try Yourself65videos
PERMUTATIONS AND COMBINATIONS
- BOOK - AAKASH INSTITUTECHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section A Objective type questions (One option is correct )51videos
PERMUTATIONS AND COMBINATIONS
- BOOK - AAKASH INSTITUTECHAPTER - MATRICESEXERCISE - Assignment (Section - J) Aakash Challengers Questions3videos
MATRICES
- BOOK - AAKASH INSTITUTECHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)12videos
PRINCIPLE OF MATHEMATICAL
Similar Questions
The letters of the word 'RANDOM' are written in all possible orders and these words are written out as in dictionary. Find the rank of the word 'RANDOM'.
View SolutionIf the letters of the word ‘MOTHER’ are written in all possible orders and these words are written out as in a dictionary, find rank of the word ‘MOTHER’.
View SolutionThe letters of word ZENITH are written in all possible ways. If all these words are written out as in a dictionary, then find the rank of the word ZENITH.
View SolutionIf all the letters of the word 'KRISHNA' are arranged in all possible ways and these words are written out as in a dictionary, then the rank of the word 'KRISHNA' is :
View SolutionIf the letters of the word KRISHNA are arranged in all possible ways and these words are written out as in a dictionary, then the rank of the word KRISNA is
View SolutionIf the letters of the word MOTHER are arranged in all possible ways and these words are written out as in a dictionary, then the rank of the word MOTHER is
View SolutionIf the letters of the word VERMA are arranged in all possible ways and these words are written out as in a dictionary, then the rank of the word VERMA is :
View SolutionIf the letters of the word VERMA are arranged in all possible ways and these words are written out as in a dictionary, then the rank of the word VERMA is :
View SolutionIf the letters of the word KRISNA are arranged in all possible ways and these word 23 written out as in a dictionary, then the rank of the word KRISNA is
View SolutionThe letters of word ZENITH are written in all possible ways. If all these words are written in the order of a dictionary then the rank of the work ZENITH is
View Solution