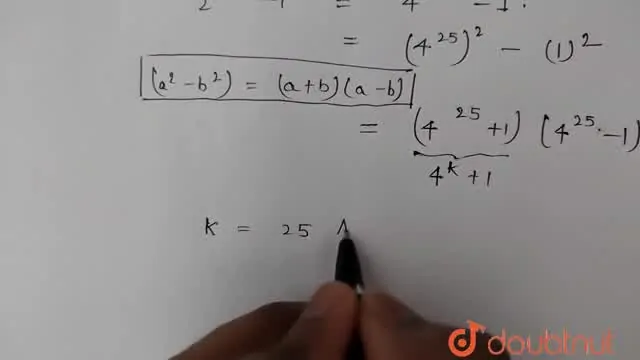The greatest +ve integer k, for which 4k+1 is factor of sum 1+2+22+....+299 is
Video Solution
Text Solution
The correct Answer is:25
1+2+22+...299=2100−1
=450−1=(425−1)(425+1)
∴k=25.
|
Updated on:21/07/2023
Related Playlists
Similar Questions
The greatest positive integer k, for which 81k+1 is a factor of the sum 9350+9346……94+92+1
View SolutionThe greatest positive integer for which 13k+1 is a factor of the sum 1371+1370+1369+….+13+1
View SolutionFind the greatest value of k for which 49k+1 is a factor of 1+49+492….(49)125
View SolutionThe largest value of the positive integer k for which nk+1 divides 1+n+n2+....+n127, is
View SolutionDetermine the value of k for which x+2 is a factor of (x+1)7+(2x+k)3.
View SolutionDetermine the value of k for which x+2 is a factor of (x+1)7+(2x+k)3.
View SolutionFind the value of k, if 2x +1 is a factor of (3k+2)x3+(k−1).
View SolutionValue of k for which x + k is a factor of the polynomial x3+kx2−2x+k+4 is
View SolutionFind the value of k, if x−1 is a factor of 4x3+3x2−4x+k .
View SolutionFind the value of k, if x−1is a factor of 4x3+3x2−4x+k.
View Solution