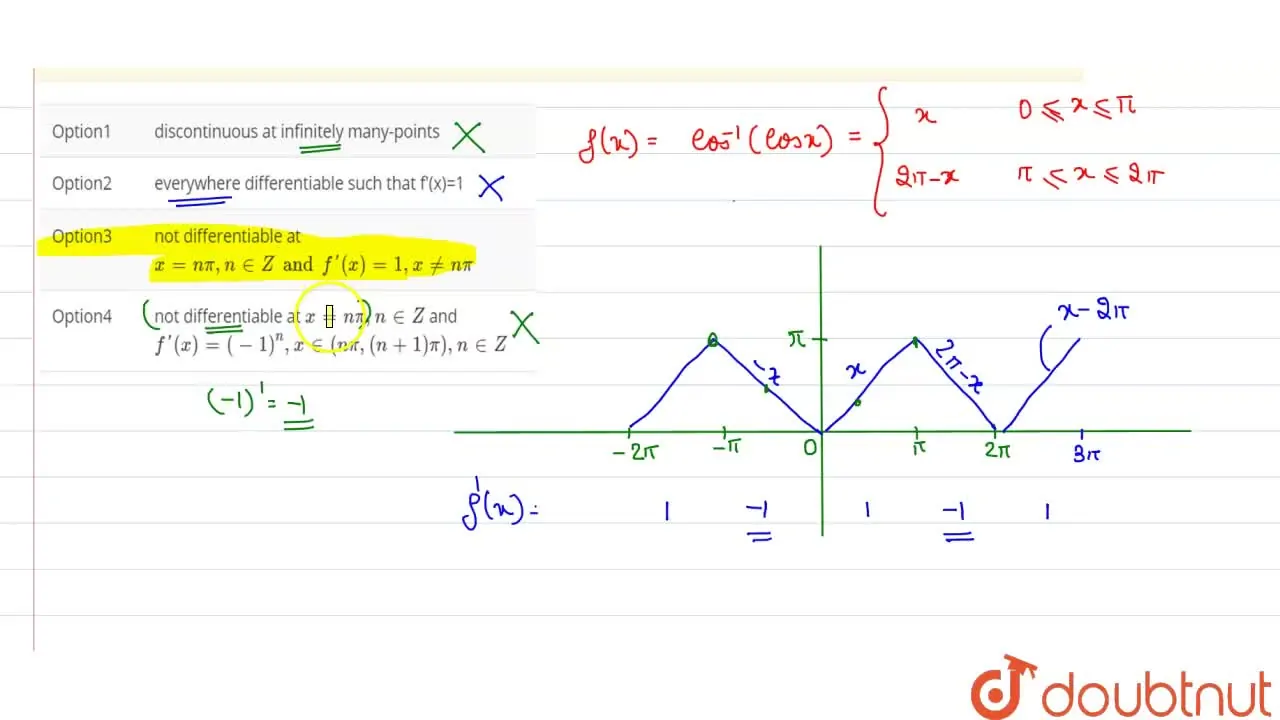
The function, f(x)=cos−1(cosx) is
discontinuous at infinitely many-points
everywhere differentiable such that f'(x)=1
not differentiable at x=nπ,n∈Zandf'(x)=1,x≠nπ
not differentiable at x=nπ,n∈Z and f'(x)=(−1)n,x∈(nπ,(n+1)π),n∈Z
The correct Answer is:D
The graph of the f(x)=cos−1 (cos x) as given in Fig.6
It is evident from the curve y=f(x) that f(x) is everywhere continuous but it is not differentiable x=n,n∈Z
Also, f'(x)=(−1)n,x∈(nπ,(n+1)π),where n∈Z
We can observe that f(x) is an even periodic function with period 2π.

Related Playlists
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Section II - Assertion Reason Type13videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise87videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise87videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test58videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 256videos
DEFINITE INTEGRALS
Similar Questions
The function f(x)=sin−1(cosx)is
View SolutionThe domain of the function f(x)=cos−1(x+[x]) is
View SolutionThe domain of the function f(x)=cos−1(2−|x|4) is
View SolutionThe maximum ordinate of a point on the graph of the function f(x) = sin x( 1+ cos x ) is
View SolutionThe domain of the function f(x)=cos−1(sec(cos−1x))+sin−1(cosec(sin−1x)) is
View SolutionThe function f(x)=sin4x+cos4x increases, if
View SolutionFind the real values of x for which the function f(x)=cos−1√x2+3x+1+cos−1√x2+3x is defined
View SolutionDomain of the function f(x)=sin−1[1+cosx]−√16−x2 ([.) denotes the greatest integer function) is
View SolutionThe function f(x)=[cosx] is
View SolutionDomain of differentiations of the function f(x) = |x -2| cos x is
View Solution