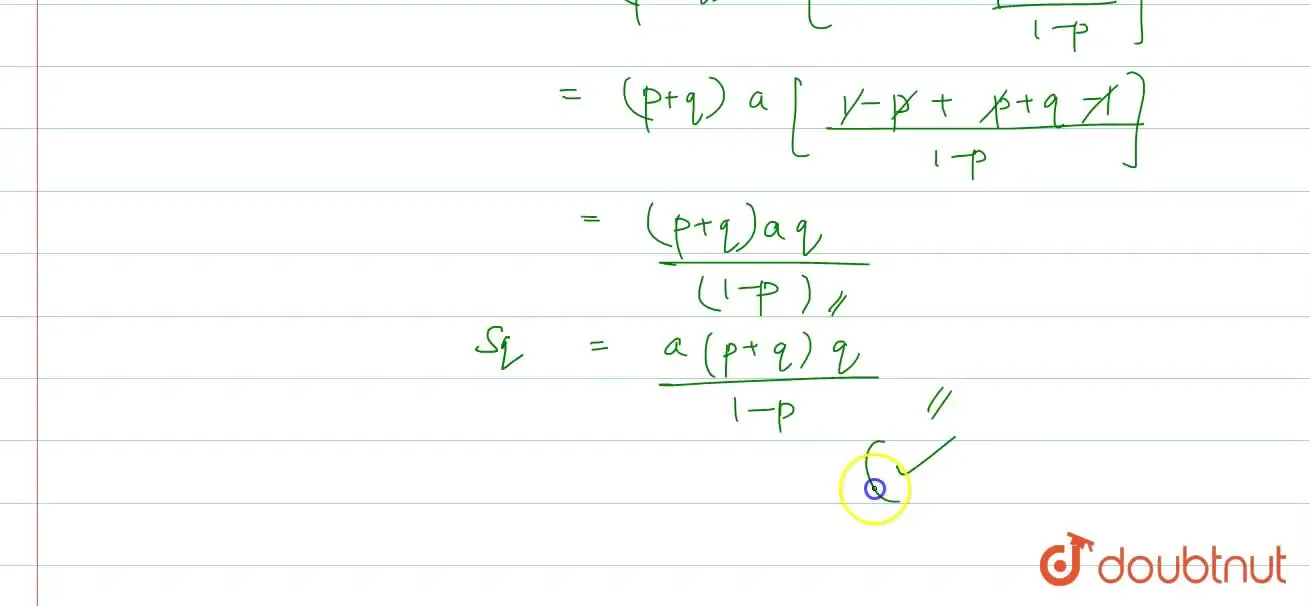The first term of an A.P. is 'a' and sum of first p terms is zero. Show that the sum of next q terms will be a(p+q)q1−p.
The correct Answer is:N/a
Let the common difference be 'd'.
Given that Sp=0 ...(1)
⇒ p2[2a+(p−1)d]=0
⇒ 2a+(p−1)d=0
⇒ d=−2ap−1=2a1−p ...(2)
Now, the sum next 'q' terms after first 'p' terms = sum of first (p+q) terms-sum of first p terms
=p+q2[2a+(p+q−1)d]−Sp
=p+q2[2a+(p+q−1).2a1−p]−0
[From eqs. (1) and (2)]
=p+q2[2a(1−p)+(p+q−1).2a1−p]
=p+q2.2a[1−p+p+q−11−p]
=a(p+q).q1−p.
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9A4videos
SEQUENCE AND SERIES
- BOOK - NAGEEN PRAKASHANCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9B17videos
SEQUENCE AND SERIES
- BOOK - NAGEEN PRAKASHANCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE12videos
RELATIONS AND FUNCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - SETSEXERCISE - MISC Exercise16videos
SETS
Similar Questions
The first term of an A.P. is a and the sum of first p terms is zero, show tht the sum of its next q terms is a(p+q)qp−1.
View SolutionIf the first term of an AP is a and the sum of the first p terms is zero, then the sum of its next q terms is
View SolutionIf the sum of p terms of an A.P. is q and the sum of q terms is p , then the sum of the p+q terms will be
View Solution7th term of an A.P. is 40. Then, the sum of first 13 terms is
View SolutionIf the sum of p terms of an A.P. is q and the sum of q terms is p, then the sum of p+q terms will be
View SolutionThe first term of an A.P. is 100 and the sum of whose first 6 terms is 5 times the sum of the next 6 terms, then the c.d. is
View SolutionThe sum of first p- terms terms of an A.P. is q and the sum of first q terms is p, find the sum of first (p + q)
View SolutionIn an AP of which 'a' is the Ist term, if the sum of the Ist p terms is equal to zero, show that the sum of the next q terms is −(aq(p+q)p−1)
View SolutionIf the sum of P terms of an A.P. is q and the sum of q terms is p , then the sum of p+q terms will be (a) 0 (b) p−q (c) p+q (d) (p+q)
View SolutionIf the first term of an A.P. is 3 and the sum of its first 25 terms is equal to the sum of its next 15 terms, then the common difference of this A.P. is:
View Solution