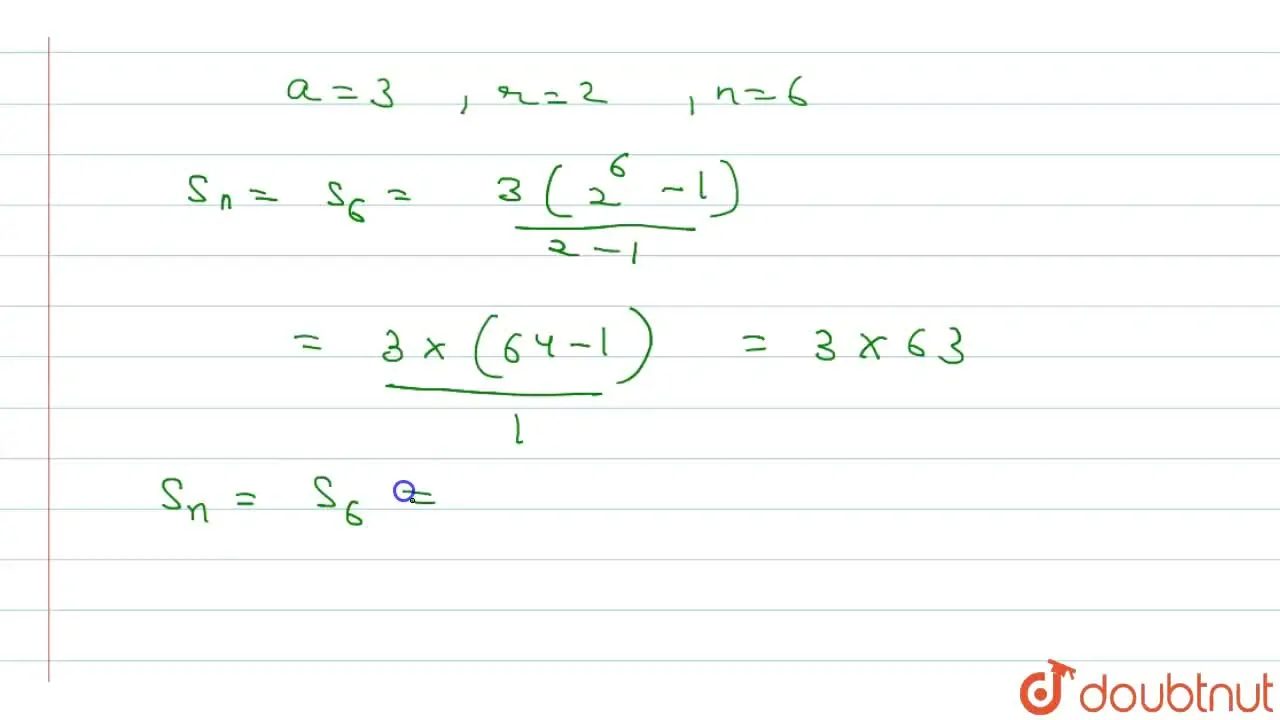The first and last term of a geometrical Pregression (G.P.) are 3 and 96 respectively. If the common ratio is 2, find :
(i) 'n' the number of terms of the G.P.
(ii) Sum of the n terms.
The correct Answer is:6, 189
Step by step video, text & image solution for The first and last term of a geometrical Pregression (G.P.) are 3 and 96 respectively. If the common ratio is 2, find : (i) 'n' the number of terms of the G.P. (ii) Sum of the n terms. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
Similar Questions
If the common ratio is −45 and the sum of infinite terms in a G.P is 809 then find the first term.
View SolutionIf the sums of the first 8 and 19 terms of an A.P. are 64 and 361 respectively, find (i) the common difference and (ii) the sum of n terms of the series.
View SolutionThe nth term of a G.P. is 3⋅2n. Find the sum of 8 terms of the G.P.
View SolutionThe 4th, 7th and last terms of a G.P. are 10,80 and 2560 respectively. Find the number of terms of the G.P.
View SolutionThe 4th and 7th terms of a G.P. are 127and1729 respectively. Find the sum of n terms of the G.P.
View SolutionThe common ratio, last term and sum of n terms of a G.P. are 2, 128 and 255 respectively. Find the value of n.
View SolutionThe fifth term of a G.P. is 32 and common ratio is
2 , then the sum of first 14 terms of the G.P. isView SolutionThe fourth, seventh, and the last term of a G.P. are 10, 80, and 2560, respectively. Find the first term and the number of terms in G.P.
View SolutionThe fourth, seventh, and the last term of a G.P. are 10, 80, and 2560, respectively. Find the first term and the number of terms in G.P.
View SolutionThe sum of some terms of a G.P. is 315 whose first term and the common ratio are 5 and 2, respectively. Find the last term and the number of terms.
View Solution