The exhaustive set of values of α2 such that there exists a tangent to the ellipse x2+α2y2=α2 and the portion of the tangent intercepted by the hyperbola α2x2−y2=1 subtends a right angle at the center of the curves is:
Equation of tangent at point P(αcosθ,sinθ) is
xαcosθ+x1sinθ=1 (1)
Let it cut the hyperbola at point P and Q.
Homogenising hyperbola α2x2−y2=1 w.r.t. line (1), we get
α2x2−y2=(xαcosθ+ysinθ)2
This is an equation of pair of straight lines OP and OQ.
Given that ∠POQ=90∘.
∴ Coefficient of x2+Coefficient of y2=0
⇒ α2−cos2θα2−1−sin2=0
⇒ α2−cos2θα2−1−1+cos2θ=0
⇒ cos2θ=α22−α2α−1
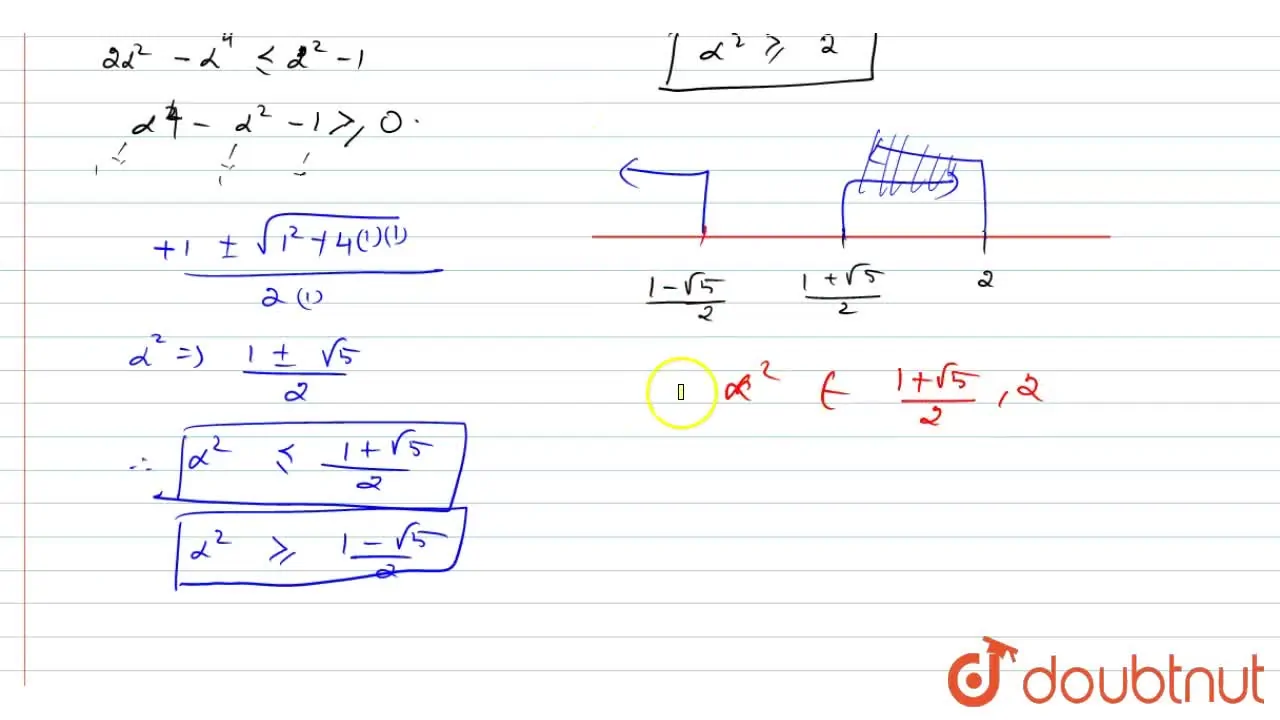
Now, 0≤cos2θ≤1
⇒ 0≤α2(2−α2)α2−1≤1
Solving, we get
α2∈[√5+12,2]
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - CONCEPT APPLICATION EXERCISE 7.13videos
HYPERBOLA
- BOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - CONCEPT APPLICATION EXERCISE 7.212videos
HYPERBOLA
- BOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE2videos
HYPERBOLA
- BOOK - CENGAGE ENGLISHCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
- BOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Multiple Correct Answer Type2videos
INDEFINITE INTEGRATION
Similar Questions
The exhaustive set value of α2 such that there exists a tangent to the ellipse x2+α2y2=α2 and the portion of the tangent intercepted by the hyperbola α2x2−y2 subtends a right angle at the center of the curves is (a)[√5+12,2] (b) (1,2] (c)[√5−12,1] (d)[√5−12,1]∪[1,√5+12]
View SolutionThe condition that the line xcosα+ysinα=p to be a tangent to the hyperbola x2/a2−y2/b2=1 is
View SolutionThe line x cos α+ysinα=p is tangent to the ellipse x2a2+y2b2=1.if
View SolutionThe line x cos α+ysinα=p is tangent to the ellipse x2a2+y2b2=1.if
View SolutionIf the line ycosα=xsinα+acosα be a tangent to the circle x2+y2=a2, then
View SolutionIf tangent of y2=x at (α,β), where β>0 is also a tangent of ellipse x12y2=1 then value of α is
View SolutionFind the set of those value(s) of α for which (7−5α4,α) lies inside the ellipse x225+y216=1
View SolutionFind the condition that the chord of contact of tangents from the point (α,β) to the circle x2+y2=a2 should subtend a right angle at the centre. Hence find the locus of (α,β).
View SolutionFind the condition that the chord of contact of tangents from the point (α,β) to the circle x2+y2=a2 should subtend a right angle at the centre. Hence find the locus of (α,β).
View SolutionIf x=2α+1 and y=α−1 is a solution of the equation 2x−3y+5=0 , find the value of α
View Solution