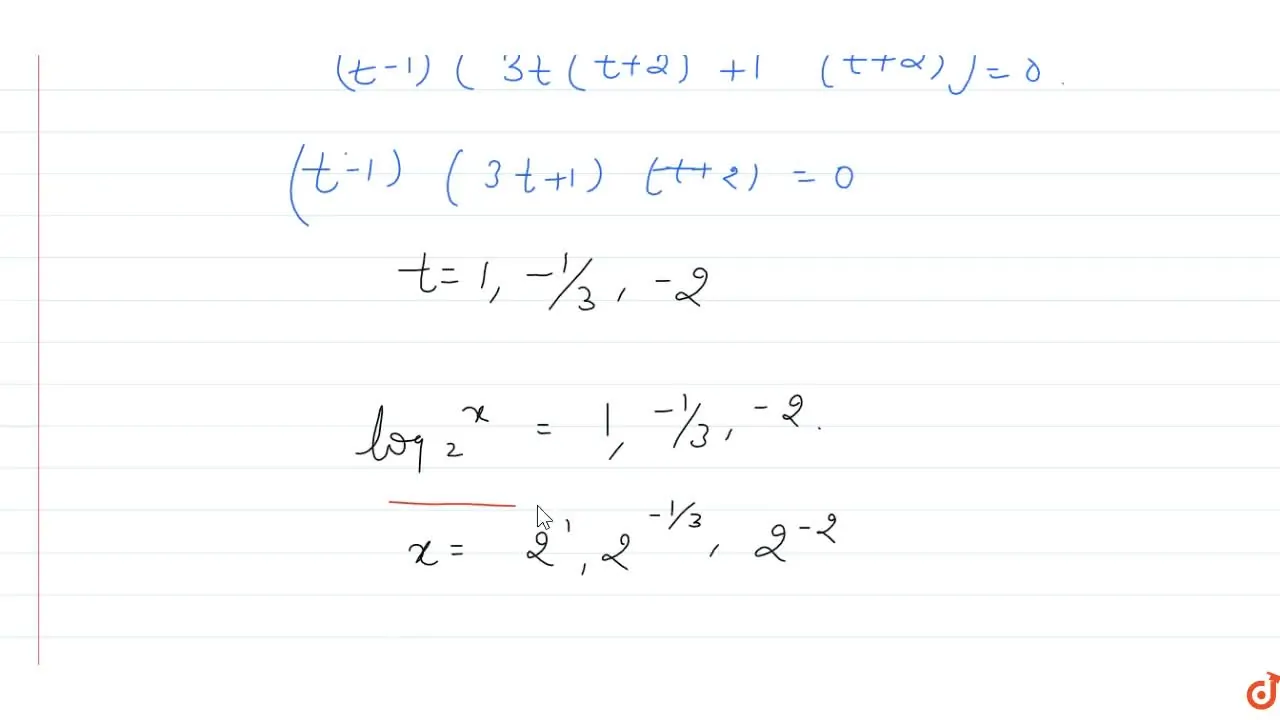The equation x(34)(log2x)2+(log2x)−(54)=√2 has (1)at least one real solution (2)exactly three solutions (3)exactly one irrational solution (4)complex roots
Video Solution
Text Solution
x(34)(log2x)2+log2x−54=√2
Taking logs both sides,
⇒((34)(log2x)2+log2x−54)log2x=log2212
⇒((34)(log2x)2+log2x−54)log2x=12
Let log2x=t
Then, equation becomes,
⇒(34t2+t−54)t=12
⇒3t3+4t2−5t−2=0
⇒(t−1)(3t2+7t+2)=0
⇒(t−1)(3t2+6t+t+2)=0
⇒(t−1)(t+2)(3t+1)=0
⇒t=1ort=−2ort=−13
⇒log2x=1orlog2x=−2orlog2x=−13
⇒x=21,2−13,2−2
So, there are exactly three solutions for x.
|
Updated on:21/07/2023
Related Playlists
Similar Questions
The equation x34(log2x)2+log2x−54=√2 has :
View SolutionThe equation x34(log2x)2+log2x−54=√2 has :
View SolutionThe equation x34((log)2x)2+(log)2x−54=√2 has (1989, 2M) at least one real solution exactly three real solutions exactly one irrational solution complex roots
View Solutionsolve the equation x34(log2x)2+log2x−54=√2
View Solutionif x34(log3x)2+log3x−54=√3 then x has
View Solutionif x34(log3x)2+log3x−54=√3 then x has
View SolutionIf x34(log3x)2+log3x−54=√3 then x has
View SolutionIf x34(log3(x))2+log3(x)−54=√3 then x has
View SolutionFor the equation x34(log2x)2+log2(x)−54=√2 which one of the following is not true?
View SolutionIf x{34(log3x)2+(log3x)−54}=√3, then x has
View Solution