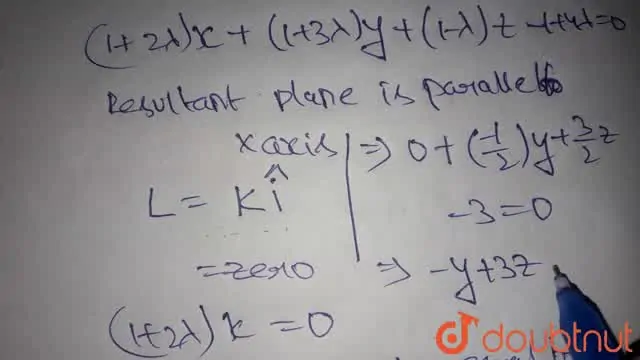
The equation of the plane through the intersection of the planes x+y+z=1 and 2x+3y−z+4=0 and parallel to x-axis is
y−3z+6=0
3y−z+6=0
y+3z+6=0
3y−2z+6=0
The correct Answer is:(a)
Step by step video & image solution for The equation of the plane through the intersection of the planes x+y+z=1 and 2x+3y-z+4 = 0 and parallel to x-axis is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - JEE Type Solved Examples : Matching Type Questions4videos
THREE DIMENSIONAL COORDINATE SYSTEM
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise For Session 112videos
THREE DIMENSIONAL COORDINATE SYSTEM
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)35videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)12videos
TRIGONOMETRIC EQUATIONS AND INEQUATIONS
Similar Questions
Find the equation of the plane passing through the intersection of the planes 4x−y+z=10 and x+y−z=4 and parallel to the line with direction ratios proportional to 2, 1, 1.
View SolutionThe equation of the plane passing through the line of intersection of the planes x+y+z+3=0and2x−y+3z+2=0 and parallel to the line x1=y2=z3 is
View SolutionThe equation of the plane passing through the intersection of the planes 2x−5y+z=3 and x+y+4z=5 and parallel to the plane x+3y+6z=1 is x+3y+6z=k, where k is
View SolutionSTATEMENT-1 : The equation of the plane through the intersection of the planes x+y+z=6 and
29x+23y+17z=276 and passing through (1,1,1), is 5x+4y+3z=47
and
STATEMENT-2 : Equation of the plane through the line of intersection of the planes P1=0andP2=0 is
P1+λP2=0,λ≠0,View SolutionFind the equation of the plane through the intersection of the planes 3x−4y+5z=10and2x+2y−3z=4 and parallel to the line x=2y=3z.
View SolutionFind the equation of the plane through the intersection of the planes 3x−4y+5z=10and2x+2y−3z=4 and parallel to the line x=2y=3z.
View SolutionFind the equation of plane through the line of intersection of the planes 3x – 4y + 5z = 10, 2x +2y-3z=4 and parallel to the line x=2y=3z
View SolutionFind the equation of the plane through the intersection of the planes 3x−y+2z−4=0andx+y+z−2=0 and the point (2,2,1).
View SolutionThe equation of the plane through the line of intersection of the planes ax+by+cz+d=0 and a'x+b'y+c'z+d'=0 parallel to the line y=0 and z=0 is
View SolutionThe equation of the plane through the line of intersection of the planes ax+by+cz+d=0 and a'x+b'y+c'z+d'=0 parallel to the line y=0 and z=0 is
View Solution