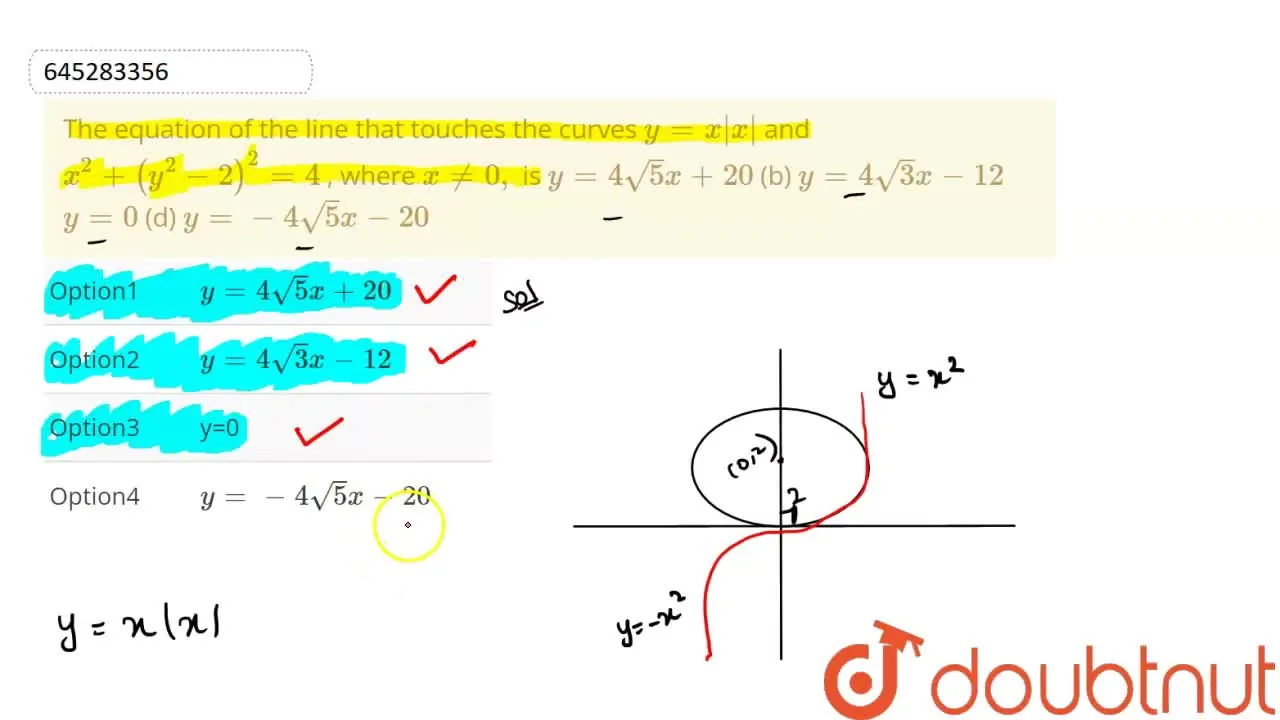
The equation of the line that touches the curves y=x|x| and x2+(y2−2)2=4 , where x≠0, is y=4√5x+20 (b) y=4√3x−12 y=0 (d) y=−4√5x−20Solution in Tamil
y=4√5x+20
y=4√3x−12
y=0
y=−4√5x−20
The correct Answer is:A, B, C
1,2,3

y=x|x|={x2,x≥0−x2,x<0
y=mx+c
If it touches y=x2,x≥0 then mx+c=x2 has equal roots, i.e.,
m2+4c=0orc=−m24 (2)
Also, the line touches the circle. Therefore,
|0−2+c|√m2+1=2 (3)
or4−4c+c2=4(1−4c)
c2+12c=0
i.e., c=0or−12
For c=0, m=0
Therefore, the equation of tangent is y=√48x−12.
If line (1) touches y=−x2,x<0, then the equation mx+c=−x2 has equal roots. Therefore,
D=0
orm2−4c=0 (4)
From (3) and (4), we get
c220c=0
∴c=0orc=20
For c=20,m=√80
Therefore, the equation of tangent is y=√80x+20
Related Playlists
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Comprehension)41videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Matrix)4videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Single)98videos
PARABOLA
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank4videos
PERMUTATION AND COMBINATION
Similar Questions
A tangent is drawn at any point P(t) on the parabola y2=8x and on it is takes a point Q(α,β) from which a pair of tangent QA and OB are drawn to the circle x2+y2=8. Using this information, answer the following questions :
The locus of circumcenter of ΔAQB id t=2 is07:59View SolutionConsider the parabola (x−1)2+(y−2)2=(12x−5y+3)2169 and match the following lists :
 08:35View Solution
08:35View SolutionWhich one of the following equation represent parametric equation to a parabolic curve? (a) x=3cost;y=4sint (b) x2−2=2cost;y=4cos2t2 (c)√x=tant;√y=sect (d) x=√1−sint;y=sint2+cost2
02:56View SolutionThe distance between the lines (x+7y)2+4√2(x+7y)−42=0 is_____________
04:48View SolutionIf the number of ways in which a selection of 100 balls can be made out of 100 identical red balls, 100 identical blue balls and 100 identical white balls is
13:22View SolutionThe area bounded by the curves y=cosxandy=sinx between the ordinates x=0andx=3π2 is (1) 4√2+2 (2) 4√21 (3) 4√2+1 (4) 4√22
01:59View SolutionThe equation of the line that touches the curves y=x|x| and x2+(y−2)2=4 , where x≠0, is (a)y=4√5x+20 (b)y=4√3−12 (c)y=0 (d) y=−4√5x−20
05:50View SolutionEquation of a circle of radius 2 and touching the circles x2+y2−4|x|=0 is x2+y2+2√3y+2=0 x2+y2+4√3y+8=0 x2+y2−4√3y+8=0 none of these
03:31View SolutionThe value of f(x,y)=((4sqrt(x^(3)y)-4sqrt(x^(3)))/(sqrt(y)-sqrt(x))+(1+sqrt(xy))/(4sqrt(xy)))^(-2)(1+2sqrt((y)/(x))+(y)/(x))^((1)/(2)) when x=9,y=0.04
03:29View SolutionThe shortest distance between the parabola y2=4x and the circle x2+y2+6x−12y+20=0 is : (A) 0 (B) 1 (C) 4√2−5 (D) 4√2+5
08:41View SolutionFind the distance between the parallel lines x+4√3y+10=0 and x+4√3y−18=0.
07:04View SolutionThe shortest distance between the line x=y and the curve y2=x−2 is
02:15View SolutionThe angle between the pair of lines 3(x−4)2+4√3(x−4)(y+2)−2(y+2)2=0 is
06:32View SolutionThe area bounded by the curves y=cosxandy=sinx between the cordinates x=0andx=3π2 is (1) 4√2−2 (2) 4√21 (3) 4√2+1 (4) 4√22
15:27View SolutionLine x+y+ 4sqrt(6) = 0 And line pair x^(2)-4xy + y^(2)=0 The triangle formed with-
03:58View Solution