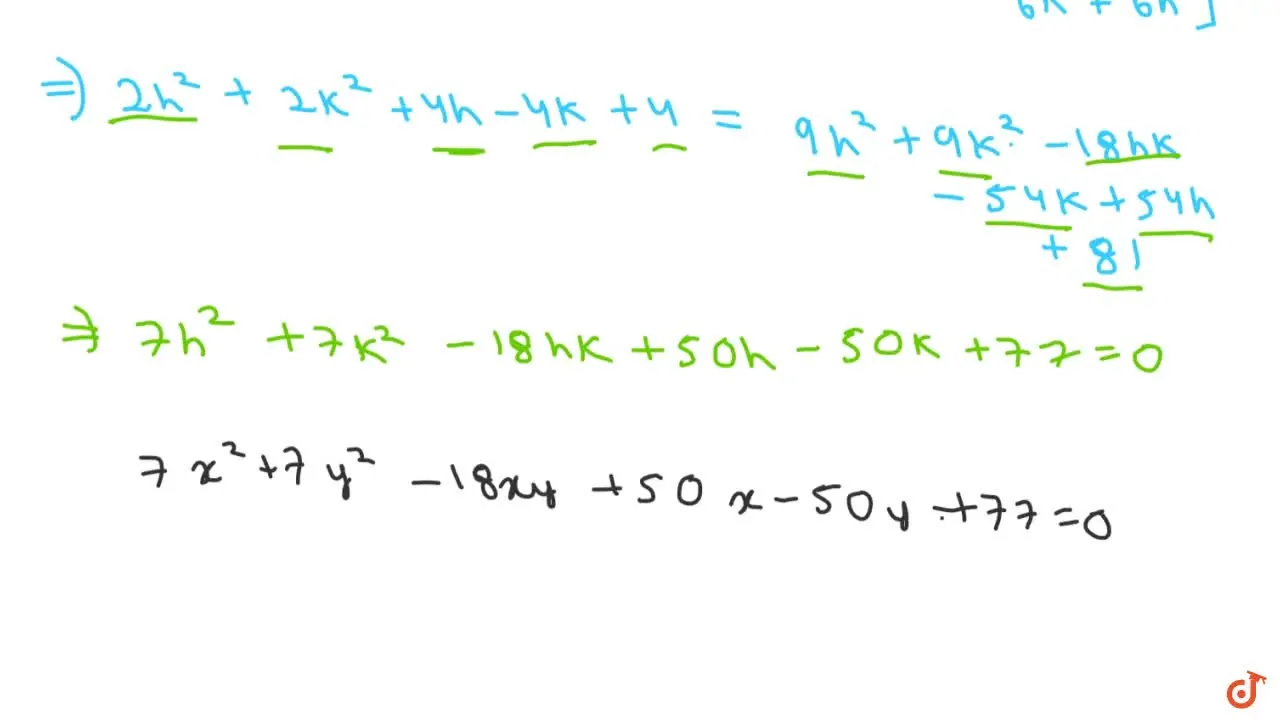The equation of the directrix of a hyperbola is Its focus is (-1,1) and eccentricity 3. Find the equation of the hyperbola.
Let be a point on the hyperbola.
And we know that,
Distance of point from focus Eccentricity Distance of point from directrix.
This is the required equation of the hyperbola.
Related Playlists
Similar Questions
The equation of one of the directrices a hyperbola is 2x + y=1,the corresponding focus is (1, 2), and e=√3. Find the equation of the hyperbola and the coordinates of the center and the second focus.
View SolutionThe equation of directrix of a hyperbola is 3x+4y+8=0 The focus of the hyperbola is (1,1). If eccentricity of the hyperbola is 2 and the length of conjugate axis is k then [k], where [] represents the greatest integer function, is equal to ________ .
View SolutionThe equation of the hyperbola whose directrix is 2x+y=1, focus (1,1) and eccentricity =√3, is
View SolutionFind the equation of the hyperbola whose directrix is 2x+y=1, focus(1,2) and eccentricity √3.
View SolutionFind the equation of the hyperbola whose one focus is (−1,1) , eccentricity = 3 and the equation of the corresponding directrix is x−y+3=0 .
View SolutionFind the equation of the hyperbola whose diretrix is 2x+y=1, focus (1, 2) and eccentricity √3.
View SolutionIf the focus =(2,3)and directrix is x+y=1 then the equation of the parabola is ____.
View SolutionFind the equation of the hyperbola whose : focus is (1,1) directrix is 3x+4y+8=0 and eccentricity =2
View SolutionFind the equation of the hyperbola whose : focus is (2,-1) directrix is 2x+3y=1 and eccentricity =2
View SolutionThe equation of the hyperbola whose directrix x+2y=1, focus (2,1) and eccentricity 2, is
View Solution