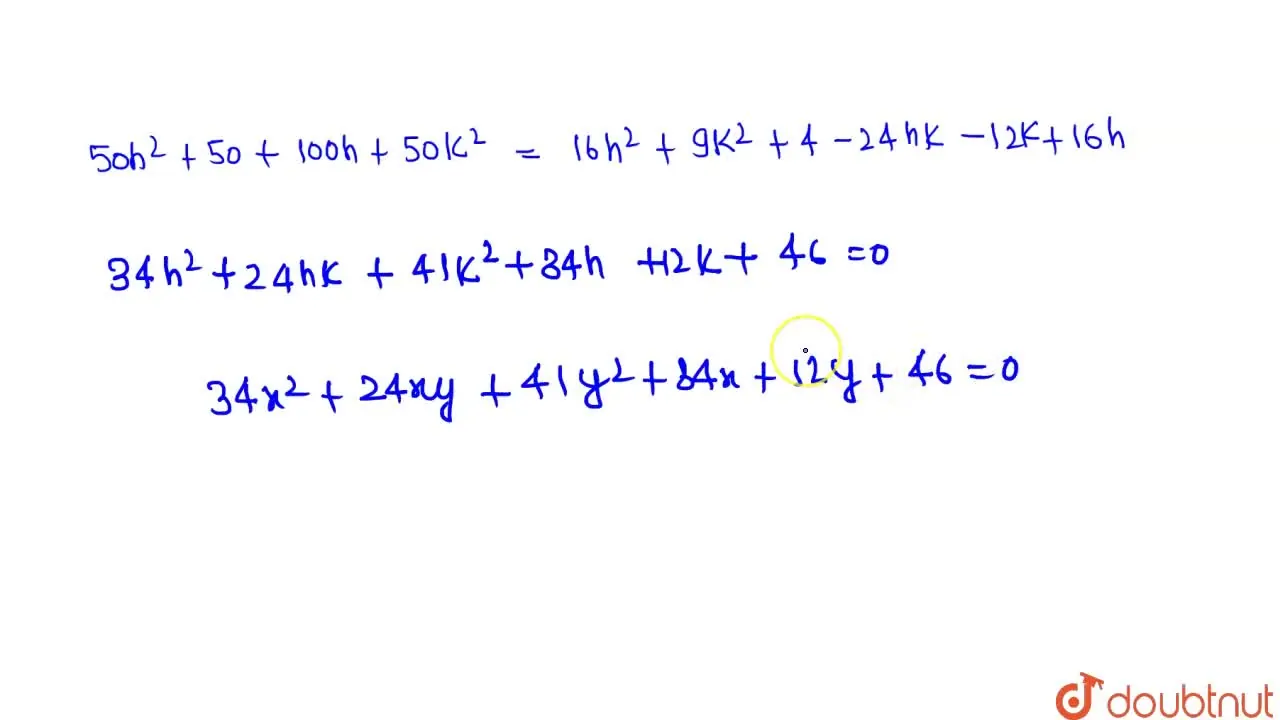The equation of conic section whose focus is at (-1 , 0), directrix is the 4x−3y+2=0 and eccentricity 1/√2, is
34x2+41y2+24xy+84x+12y+46=0
34x2+41y2−24xy+84x+12y+46=0
34x2+41y2−24xy−84x−12y+46=0
none of these.
The correct Answer is:A
Let P (h, k) be a point of the conic. Then, by difinition
SP=e PM
⇒ √(h+1)2+(k−0)2=1√2∣4h−3k+2√42+(3)2
⇒ (h+1)2+k2=150(4h−3k+2)2

So, the locus of (h, k) is
(x+1)2+y2=150(4x−3y+2)2
⇒ 50{(x+1)2+y2}=(4x−3y+2)2
⇒ 34x2+41y2+24xy+84x+12y+46=0
Hence, the equation of the conic is
34x2+24xy+41y2+84x+12y+46=0
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - PARABOLAEXERCISE - Section I - Solved Mcqs66videos
PARABOLA
- BOOK - OBJECTIVE RD SHARMACHAPTER - PARABOLAEXERCISE - SECTION-I (SOLVED MCQs EXAMPLE)1videos
PARABOLA
- BOOK - OBJECTIVE RD SHARMACHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Chapter Test19videos
PAIR OF STRAIGHT LINES
- BOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Chapter Test60videos
PERMUTATIONS AND COMBINATIONS
Similar Questions
The equation of conic section whose focus is at (-1 , 0), directrix is the 4x−3y+2=0 and eccentricity 1/√2, is
View SolutionThe equation of the hyperbola whose focus is (1,2), directrix is the line x+y+1=0 and eccentricity 3/2, is
View SolutionThe equation of an ellipse whose focus is (−1,1), directrix is x−y+3=0 and eccentricity is 12, is given by
View SolutionThe equation of the ellipse whose focus is (1,-1), directrix x−y−3=0 and eccentricity equals 12 is :
View Solutionthe equation of the ellipse whose foucs is S(1,-1) directrix the line x−y−3=0 and eccentricity1/2, is
View SolutionThe equation of the conic with focus at (1,−1), directrix along x−y+1=0 and with eccentricity √2, is
View SolutionThe equation of the ellipse whose focus is (1,0) and the directrix is x+ y+1=0 and eccentricity is equal to 1/√2 is
View SolutionFind the equation to the ellipse whose one focus is (2, 1), the directrix is 2x−y+3=0 and the eccentricity is 1√2
View SolutionFind the equation of the hyperbola whose : focus is (1,1) directrix is 2x+y=1 and eccentricity =√3
View SolutionFind the equation of the ellipse whose focus is (1,0), the directrix is x+y+1=0 and eccentricity is equal to 1√2.
View Solution