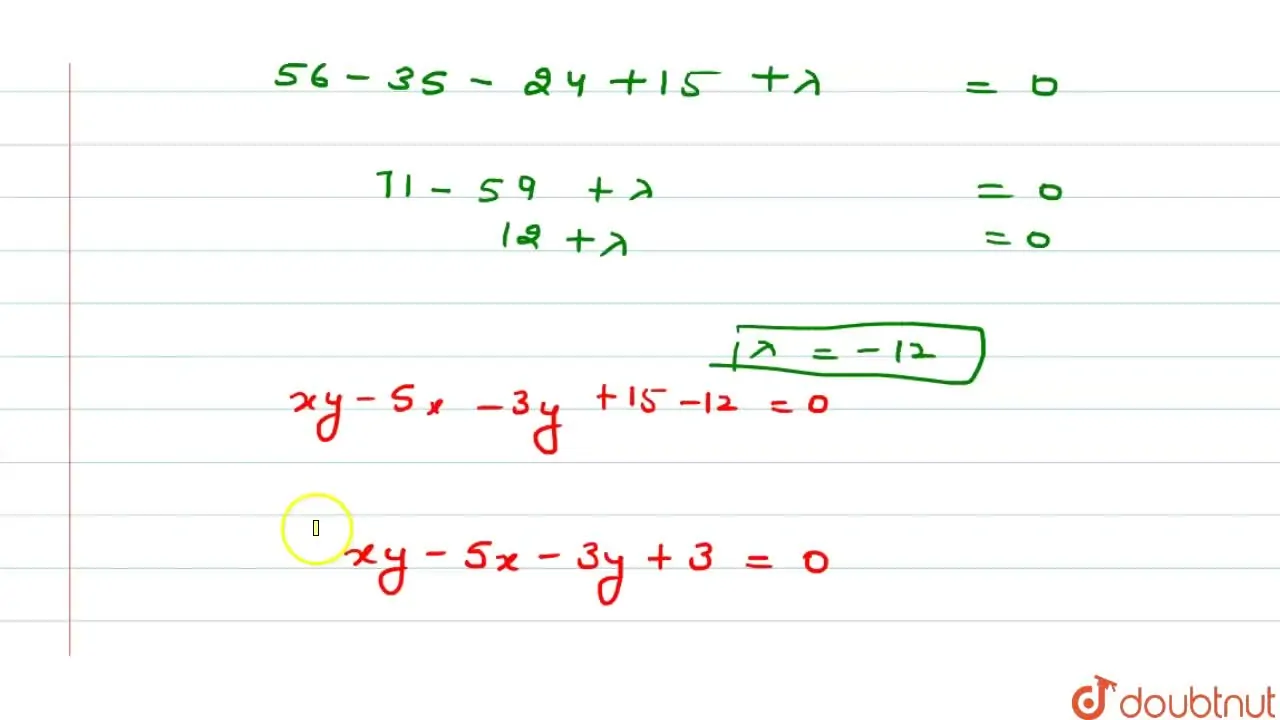The equation of a rectangular hyperbola whose asymptotes are and and passing through (7,8) is (a) (b) (c) (d)
The correct Answer is:D
The equation of the rectangular hyperbola is
It passes through (7, 8). Hence,
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - MULTIPLE CORRECT ANSWERS TYPE18videos
HYPERBOLA
- BOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - COMOREHENSION TYPE21videos
HYPERBOLA
- BOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - CONCEPT APPLICATION EXERCISE 7.64videos
HYPERBOLA
- BOOK - CENGAGE ENGLISHCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
- BOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Multiple Correct Answer Type2videos
INDEFINITE INTEGRATION
Similar Questions
The equation of a rectangular hyperbola whose asymptotes are x=3 and y=5 and passing through (7,8) is xy−3y+5x+3=0 xy+3y+4x+3=0 xy−3y+5x−3=0 xy−3y+5x+3=0
View SolutionFind the equation of a hyperbola whose asymptotes are 2x−y−3=0and3x+y−7=0 and which pass through (1,1).
View SolutionFind the vertices of the triangle whose sides are y+2x=3,4y+x=5and5y+3x=0
View SolutionThe equation of the asymptotes of a hyperbola are 4x−3y+8=0 and 3x+4y−7=0, then
View SolutionThe center of a rectangular hyperbola lies on the line y=2x. If one of the asymptotes is x+y+c=0 , then the other asymptote is 6x+3y−4c=0 (b) 3x+6y−5c=0 3x−6y−c=0 (d) none of these
View SolutionThe center of a rectangular hyperbola lies on the line y=2x. If one of the asymptotes is x+y+c=0 , then the other asymptote is 6x+3y−4c=0 (b) 3x+6y−5c=0 3x−6y−c=0 (d) none of these
View SolutionFind the equation of the hyperbola, whose asymptotes are the straight lines (x+2y+3)=0,(3x+4y+5)=0 and which passes through the point (1-1).
View SolutionIf the foci of a hyperbola lie on y=x and one of the asymptotes is y=2x, then the equation of the hyperbola, given that it passes through (3, 4), is (a)x2−y2−52xy+5=0 (b) 2x2−2y2+5xy+5=0 (c) 2x2+2y2−5xy+10=0 (d) none of these
View SolutionThe equation of tangent to hyperbola 4x2−5y2=20 which is parallel to x−y=2 is (a) x−y+3=0 (b) x−y+1=0 (c) x−y=0 (d) x−y−3=0
View SolutionFor hyperbola whose center is at (1, 2) and the asymptotes are parallel to lines 2x+3y=0 and x+2y=1 , the equation of the hyperbola passing through (2, 4) is (a) (2x+3y−5)(x+2y−8)=40 (b) (2x+3y−8)(x+2y−8)=40 (c) (2x+3y−8)(x+2y−5)=30 (d) none of these
View Solution