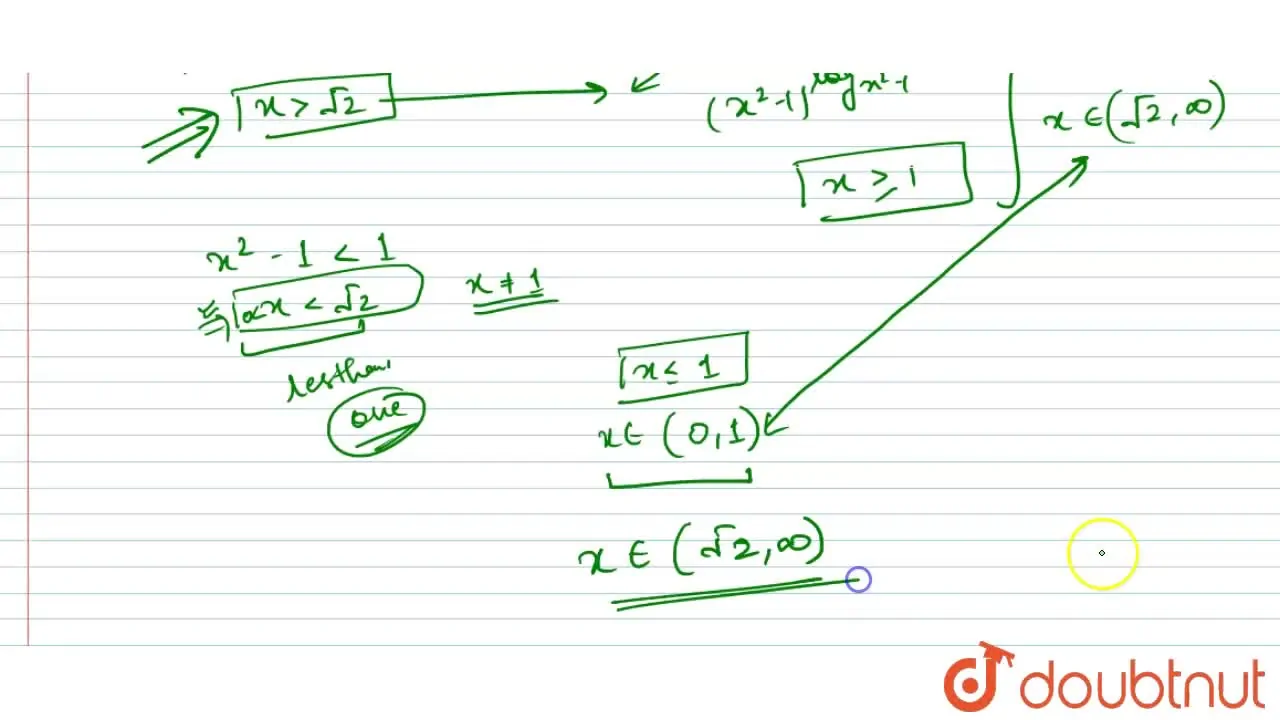
The domain of definition of the function f(x)=√logx2−1x is
(√2,∞)
(0,∞)
(1,∞)
none of these
The correct Answer is:A
We have,
f(x)=√log(x2−1)x
Clearly,f(x) is define,if
log(x2−1)x≥0,x≥0,x2≥−1≥0andx2−1≠1
Now,
log(x2−1)x>0
⇒{x>1ifx2−1>10<x<1ifx2−1<1
⇒{x≥1ifx2−2<00<x<1ifx2−2<0
⇒{x≥1ifx<−√2or,x>√20<x<1if−√2<x<√2
⇒x>√2or,0<x<1
⇒x∈(0,1)∪(√2,∞o)
And ,
x>0,x2−1>0andx2−1≠1
⇒x∈(1,√2)
From (i) and (ii), we get x∈(√2,∞)
Hence, domain of f(x) is (√2,∞) .
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Section II - Assertion Reason Type8videos
REAL FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Exercise95videos
REAL FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test60videos
REAL FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test55videos
PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEM
- BOOK - OBJECTIVE RD SHARMACHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise65videos
SCALAR AND VECTOR PRODUCTS OF THREE VECTORS
Similar Questions
The domain of definition of the function f(x)=√1+log6(1−x) is
View SolutionThe domain of definition of the function f(x)=√1+log0(1−x) is :
View SolutionFind the domain of definition of the function f(x)=√x2−25
View SolutionThe domain of definition of the real function f(x)=√log12x2 of the real variable x, is
View SolutionThe domain of definition of the function f(x)=√log10(2−xx) is
View SolutionThe domain of the function f(x)=√logx2−1x is
View SolutionThe domain of definition of the function
f(x)=√log10(5x−x24) isView SolutionThe domain of definition of the real functionf(x)=√(log16x2) of the real variable x is
View SolutionThe domain of definition of the function f(x)=√3−2x−21−x+√√sin−1x, is
View SolutionFind the domain of definition of the function f(x)=√64−x2.
View Solution