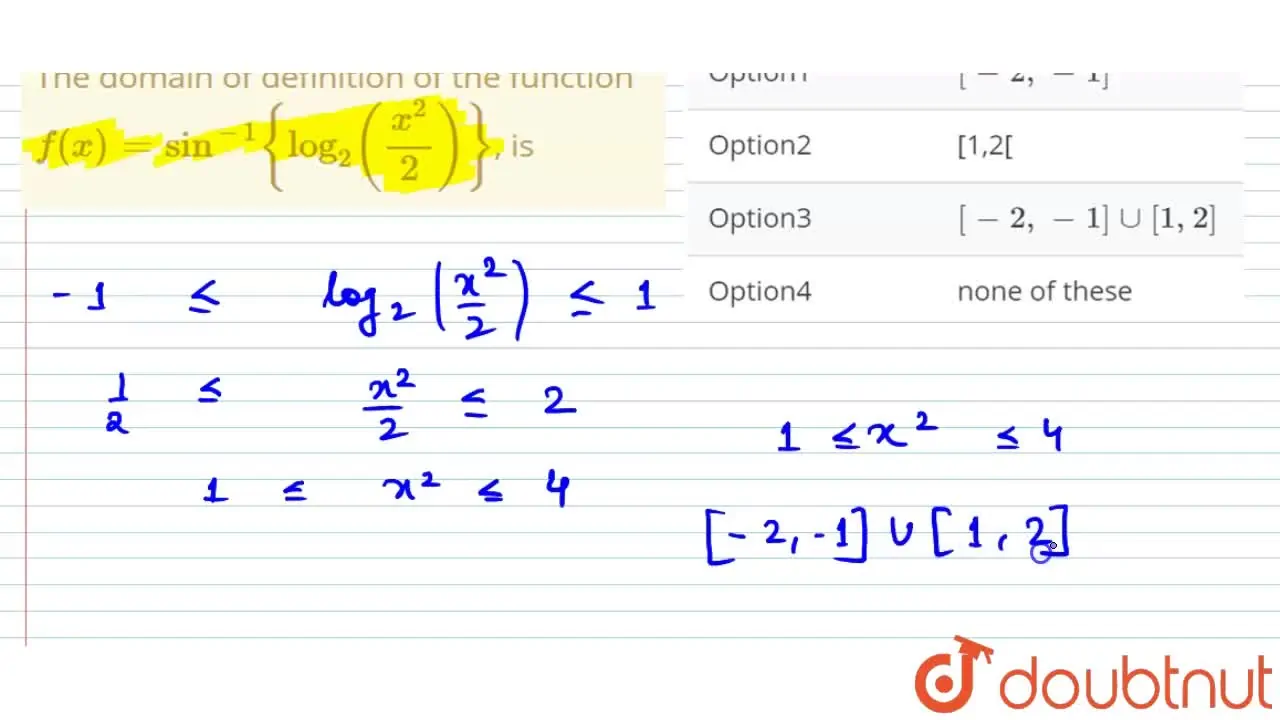
The domain of definition of the function
f(x)=sin−1{log2(x22)}, is
[−2,−1]
[1,2[
[−2,−1]∪[1,2]
none of these
The correct Answer is:C
Since the domain of sin−1x is [-1,1]. Therefore , f(x)=sin−1{log2(x22)} exists , if
−1≤log2(x2/2)≤1⇒2−1≤x22≤21
⇒1≤x2≤4⇒1≤|x|≤2⇒x∈[−2,−1]∪[1,2]
Hence , the domain of f(x) is [−2,−1]∪[1,2]
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Section I - Solved Mcqs95videos
REAL FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Section II - Assertion Reason Type8videos
REAL FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test55videos
PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEM
- BOOK - OBJECTIVE RD SHARMACHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise65videos
SCALAR AND VECTOR PRODUCTS OF THREE VECTORS
Similar Questions
The domain of definition of the function
f(x)=sin−1(|(x−1)|−2) isView SolutionThe domain of definition of the function f(x)=√1+log6(1−x) is
View SolutionThe domain of definition of the function f(x)=√logx2−1x is
View SolutionThe domain of definition of the function
f(x)=sin−1(x−32)−log10(4−x) , isView SolutionThe domain of definition of the function f(X)=x1log10x, is
View SolutionThe domain of definition of the function f(x)=√log10(2−xx) is
View SolutionThe domain of definition of the function f(x)=√1+log0(1−x) is :
View SolutionFind the domain of the function : f(x)=sin−1((log)2x)
View SolutionThe domain of definition of function of f(x)=log2(x+3)x2+3x+2 is
View SolutionThe domain of definition of the function
f(x)=√log10(5x−x24) isView Solution