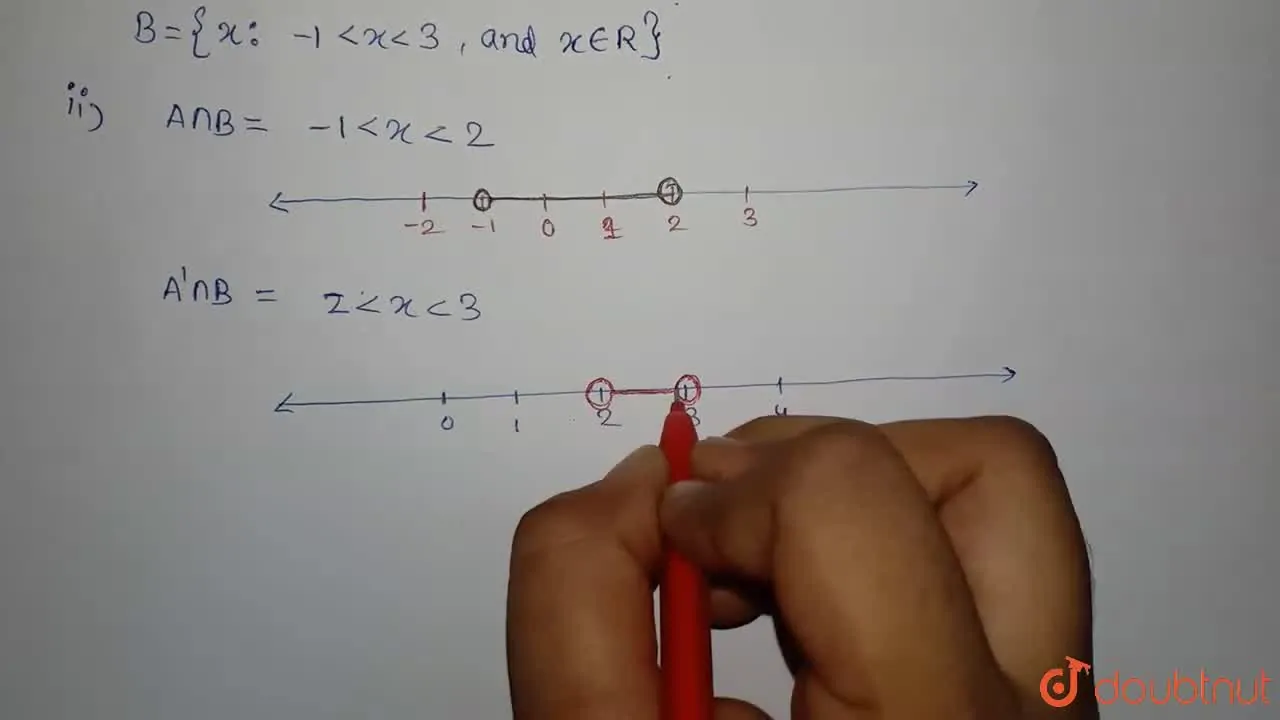The diagrams, given below, represent two inequations A and B on real number line.

(i) Write down A and B in set builder notations.
(ii) Represent A∩BandA'∩B on two different numbers lines.
The correct Answer is:A={x:−3<x<2andx∈R},B={x∈R;−<x<3}
Step by step video & image solution for The diagrams, given below, represent two inequations A and B on real number line. (i) Write down A and B in set builder notations. (ii) Represent A nn B and A' nn B on two different numbers lines. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
Similar Questions
The diagram, given below, represents two inequations P and Q on real number lines :

Write down P and Q in set builder notation.View SolutionThe diagram represents two inequation A and B on real number lines:

Write down A and B in set builder notation.View SolutionThe given diagram represents two sets A and B on real number lines.
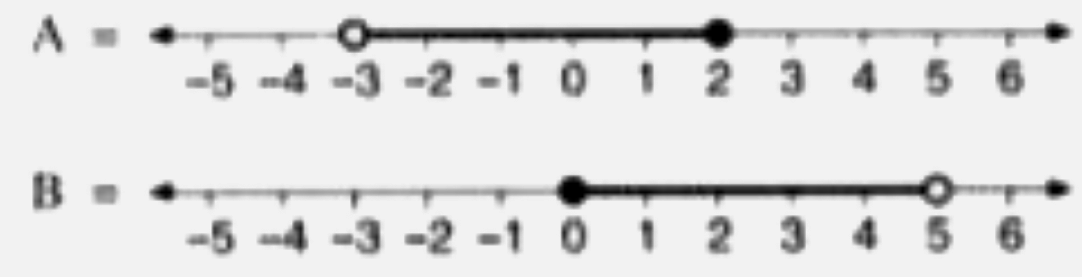
Write down A and B in set-builder notation.View SolutionThe diagram represents two inequation A and B on real number lines:
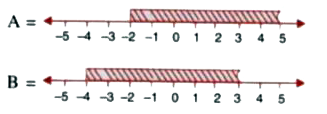
Represent A∩BandA∩B' on two different number lines.View SolutionRepresent the following inequalities on real number lines :
2x−1<5View SolutionRepresent the following inequalities on real number lines :
−2≤x<5View SolutionRepresent the following inequalities on real number lines :
−4<x<4View SolutionRepresent the following inequalities on real number lines :
2(2x−3)≤6View SolutionRepresent the following inequalities on real number lines :
3x+1≥−5View SolutionRepresent the following inequalities on real number lines :
−5<x≤−1View Solution