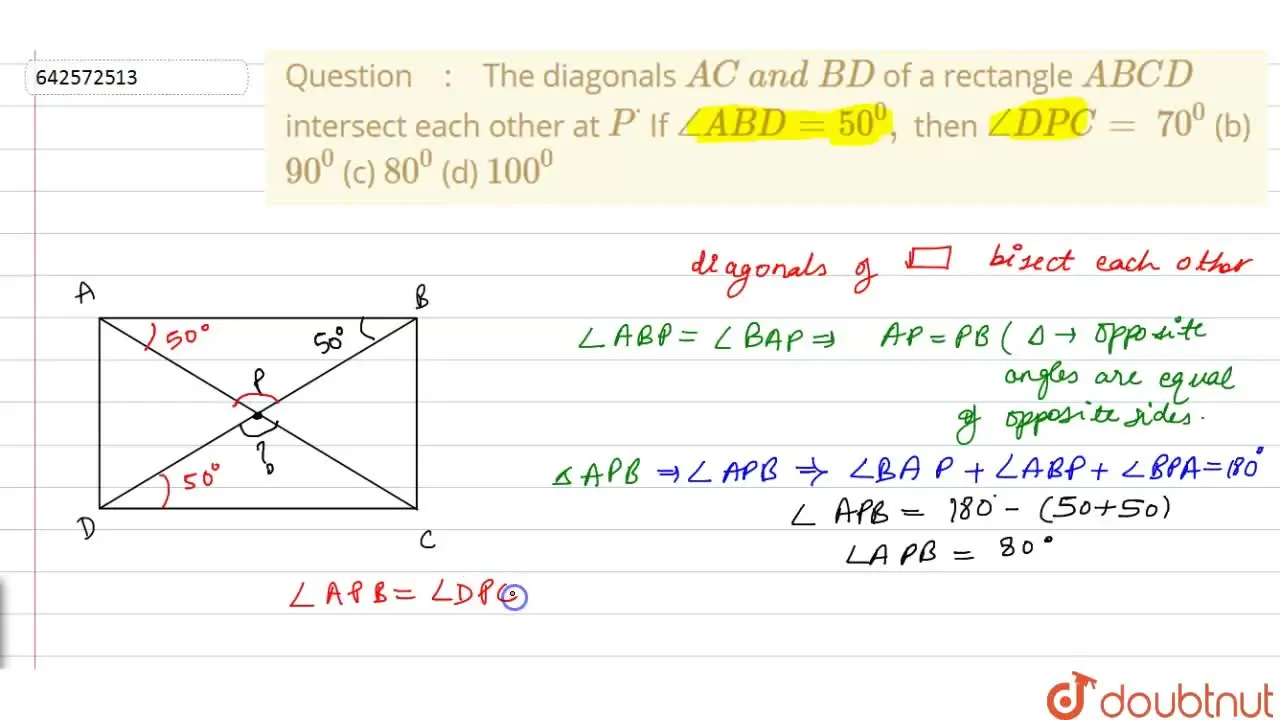
The diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD=500, then ∠DPC= 700 (b) 900 (c) 800 (d) 1000
Step by step video & image solution for The diagonals A C\ a n d\ B D of a rectangle A B C D intersect each other at Pdot If /_A B D=50^0, then /_D P C= 70^0 (b) 90^0 (c) 80^0 (d) 100^0 by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
Similar Questions
The diagonals of a rectangle ABCD intersect in O. If ∠BOC=680, find ∠ODA.
View SolutionIn Figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB=350, then ∠ADC= (a) 350 (b) 450 (c) 550 (d) 650
View SolutionDiagonals AC and BD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar (AOD)= ar (BOC) .
View SolutionIn Figure, If ∠ABC=450, then ∠AOC= (a) 450 (b) 600 (c) 750 (d) 900
View SolutionLine segments AB and CD intersect at O such that AC=DB. If ∠CAB=450and ∠CDB=550, then ∠BOD= (a)1000 (b) 800 (c) 900 (d) 1350
View SolutionThe diagonals of a parallelogram ABCD intersect at O . If ∠BOC=900 and ∠BDC=500, then ∠OAB= (a) 400 (b) 500 (c) 100 (d) 900
View SolutionTwo straight lines AB and CD intersect one another at the point O. If ∠AOC+∠COB+∠BOD=2740, then ∠AOD=
View SolutionIn a rhombus ABCD, if ∠ACB=400, then ∠ADB=(a) 700 (b) 450 (c) 500 (d) 600
View SolutionAOB is a straight line and OC and OD are the two rays on it. If ∠AOC+∠BOD=85∘, then ∠COD=
View SolutionABCD is a cyclic quadrilateral such that ∠ADB=300and ∠DCA=800, the ∠DAB= (A)700 (b) 1000 (c) 1250 (d) 1500
View Solution