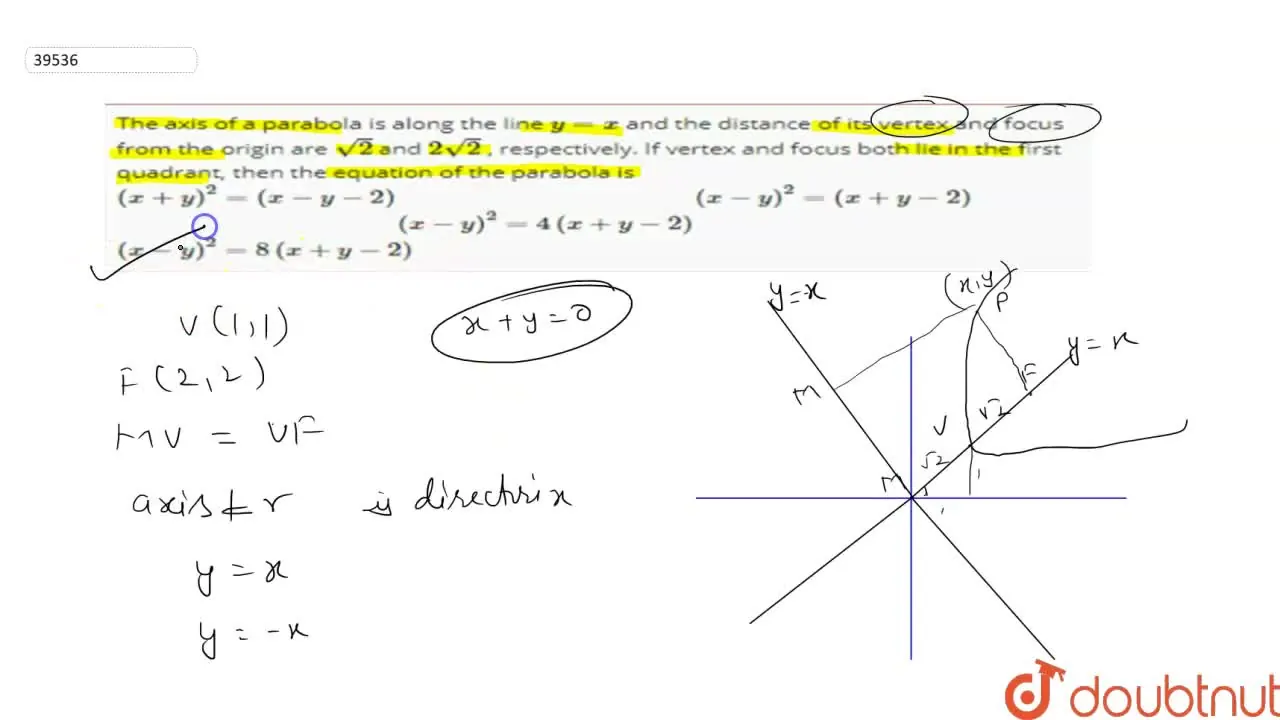
The axis of a parabola is along the line y=x and the distance of its vertex and focus from the origin are √2 and 2√2 , respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is (x+y)2=(x−y−2) (x−y)2=(x+y−2) (x−y)2=4(x+y−2) (x−y)2=8(x+y−2)
Step by step video & image solution for The axis of a parabola is along the line y=x and the distance of its vertex and focus from the origin are sqrt(2) and 2sqrt(2) , respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is (x+y)^2=(x-y-2) (x-y)^2=(x+y-2) (x-y)^2=4(x+y-2) (x-y)^2=8(x+y-2) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
The axis of parabola is along the line y=x and the distance of its vertex and focus from origin are √2 and 2√2 respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is :
View SolutionThe axis of a parabola is along the line y=x and the distance of its vertex and focus from the origin are √2 and 2√2 , respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is (x+y)2=(x−y−2) (x−y)2=(x+y−2) (x−y)2=4(x+y−2) (x−y)2=8(x+y−2)
View SolutionThe axis of a parabola is along the line y = x and the distance of its vertex from origin is √2 and that from its focus is 2√2. If vertex and focus both lie in the first quadrant, then the equation of the parabola is
View SolutionThe axis of a parabola is along the line y = x and its vertex and focus are in the first quadrant at distances √2,2√2 respectively, from the origin. The equation of the parabola, is
View SolutionFind the vertex of the parabola x2=2(2x+y)
View SolutionFind the focus of the parabola y2=8x.
View SolutionFind the focus of the parabola y2=−8x.
View SolutionFind the vertex and focus of the given parabola x2+4y=0
View SolutionA parabola has its vertex and focus in the first quadrant and axis along the line y=x . If the distances of the vertex and focus from the origin are respectively √2&2√2 , then equation of the parabola is x2+y2−8x+8y+2xy=16 x2+y2−8x−8y+16=2xy (x−y)2=8(x+y−2) (x+y)2=(x−y+2)
View SolutionThe focus of the parabola y2−x−2y+2=0 is
View Solution