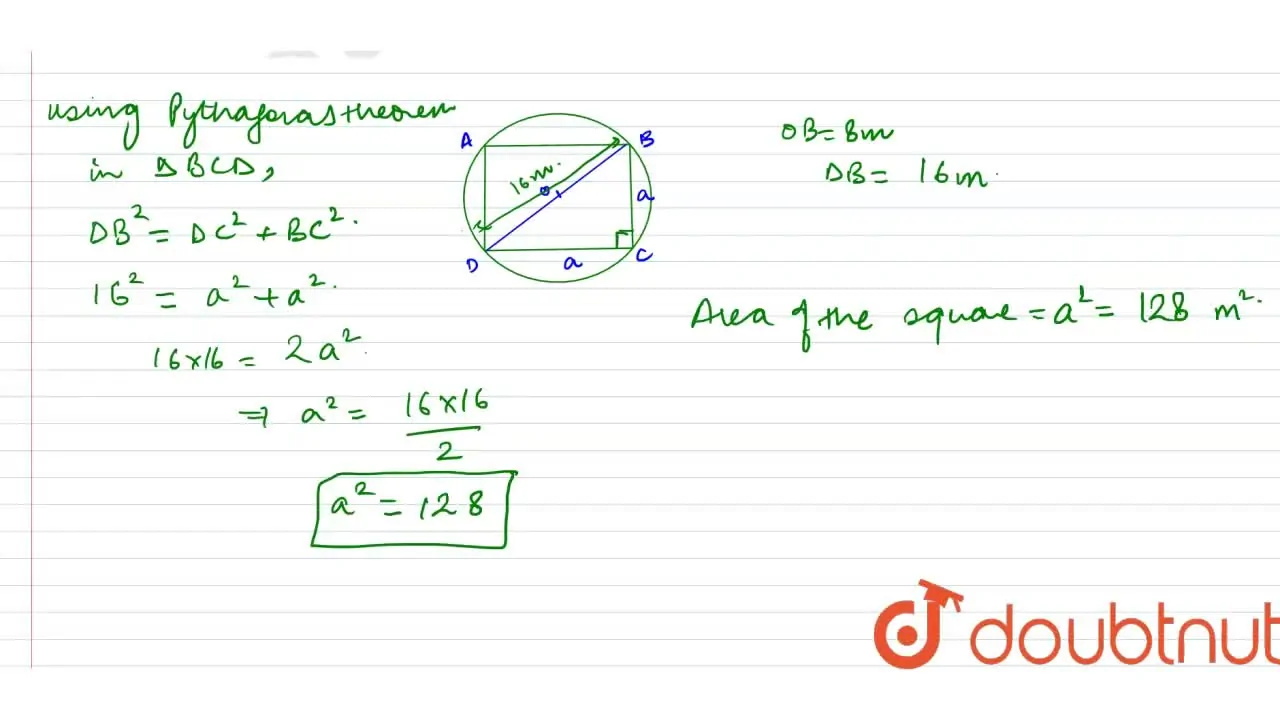
The area of the square that can be inscribed in a circle of radius 8 cm is
256 cm2
128 cm2
√2r2
64 cm2
The correct Answer is:B
Given , radius of circle, r = OC = 8cm.
∴ Diameter of the circle = AC=2×OC=2×8=16cm
Which is equal to the diagonal of a square.
Let side of square be x.
In right angled ΔABC,AC2=AB2+BC2 [by pythagoras theorem]
⇒(16)2=x2+x2
⇒256=2x2
⇒x2 = 128
∴ Area of square= x2=128cm2
Alternate Method
Radius of circle (r) = 8cm
Diameter of circle (d) = 2r=2×8=16cm
Since, square inscribed in circle.
∴ Diagonal of the squre = Diameter of circle
Now , Area of square = (Diagonal)22=(16)22=2562=128cm2
Related Playlists
Similar Questions
What is the area of the square that can be inscribed in a circle of radius 12 cm?
View SolutionWhat is the area of the largest square that can be inscribed in a circle of radius 12 cm. ?
View SolutionThe area of the square inscribed in a circle of radius 8 cm is
View SolutionThe area of a square inscribed in a circle of radius 8 cm is:
View SolutionThe area of the circle that can be inscribed in a square of side 7 cm is .................. .
View SolutionThe area of the circle that can be inscribed in a square of side 6 cm is
View SolutionThe area of an equilateral triangle inscribed in a circle of radius 4cm, is
View SolutionMaximum area of the rectangle inscribed in a circle of radius 10 cms is
View SolutionWhat is the maximum area of a rectangle that can be inscribed in a circle of radius 2 units?
View SolutionShow that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
View Solution