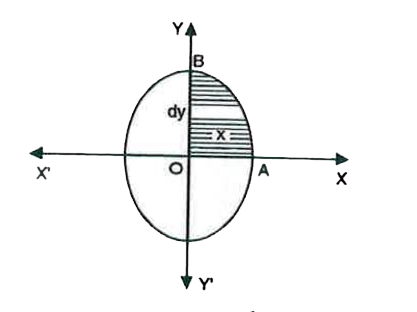
The area of the region bounded by the ellipse x225+y216=1 is
20π sq units
20π2 sq units
16π2 sq units
25π sq units
The correct Answer is:A
We have, x252+y242=1
Here, a=pm5" and "b=pm4<br>andy242=1−x252
⇒y2=16(1−x225)

⇒y=√1625(15−x2)
⇒y=45√52−x2
∴Area enclosed by ellipse,A=2.45∫5−5√52−x2dx
=2.85∫50√52−x2dx
=2.85[x2√52−x2+522sin−1.x5]50
=2.85[52√52−52+522sin−1.55−0−252.0]
=2.85[252.π2]
=165.25π4
=20π sq units
Related Playlists
Similar Questions
Find the area of the region bounded by the ellipse x29+y24=1 in fourth quadrant.
View SolutionFind the area of the region bounded by the ellipse x24+y29=1
View SolutionThe area of the region bounded by the ellipse x2/64+y2/100=1, is …….. sq. units.
View SolutionFind the area of the region bounded by the ellipse x216+y29=1.
View SolutionFind the area of the region bounded by the ellipse x2a2+y2b2=1
View SolutionFind the area of the region bounded by the ellipse x24+y29=1.
 View Solution
View SolutionFind the area of the region bounded by the ellipse x29+y24=1 in fourth quadrant.
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1.
View SolutionThe area bounded by the ellipse x24+y225=1 is
View Solution


