The area of the plane region bounded by the curve $x = y^{2} - 2$ and the line y = - x is (in sq units)

A

$\frac{13}{3}$

B

$\frac{2}{5}$

C

$\frac{9}{2}$

D

$\frac{5}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Given curvel are $x = y^{2} - 2$ and $y = - x$
On solving these two curves
$y = - (y^{2} - 2)$
$\Rightarrow y^{2} + y - 2 = 0$
$\Rightarrow y^{2} + 2 y - y - 2 = 0$
$\Rightarrow y (y + 2) - + (y + 2) = 0$
$\Rightarrow (y + 2) (y - 1) = 0$
y = 1, -2
When y = 1, then x = - 1
When y = - 2 then x = 2
Therefore intersection points of both the curves are (-1, 1) are (2, -2)

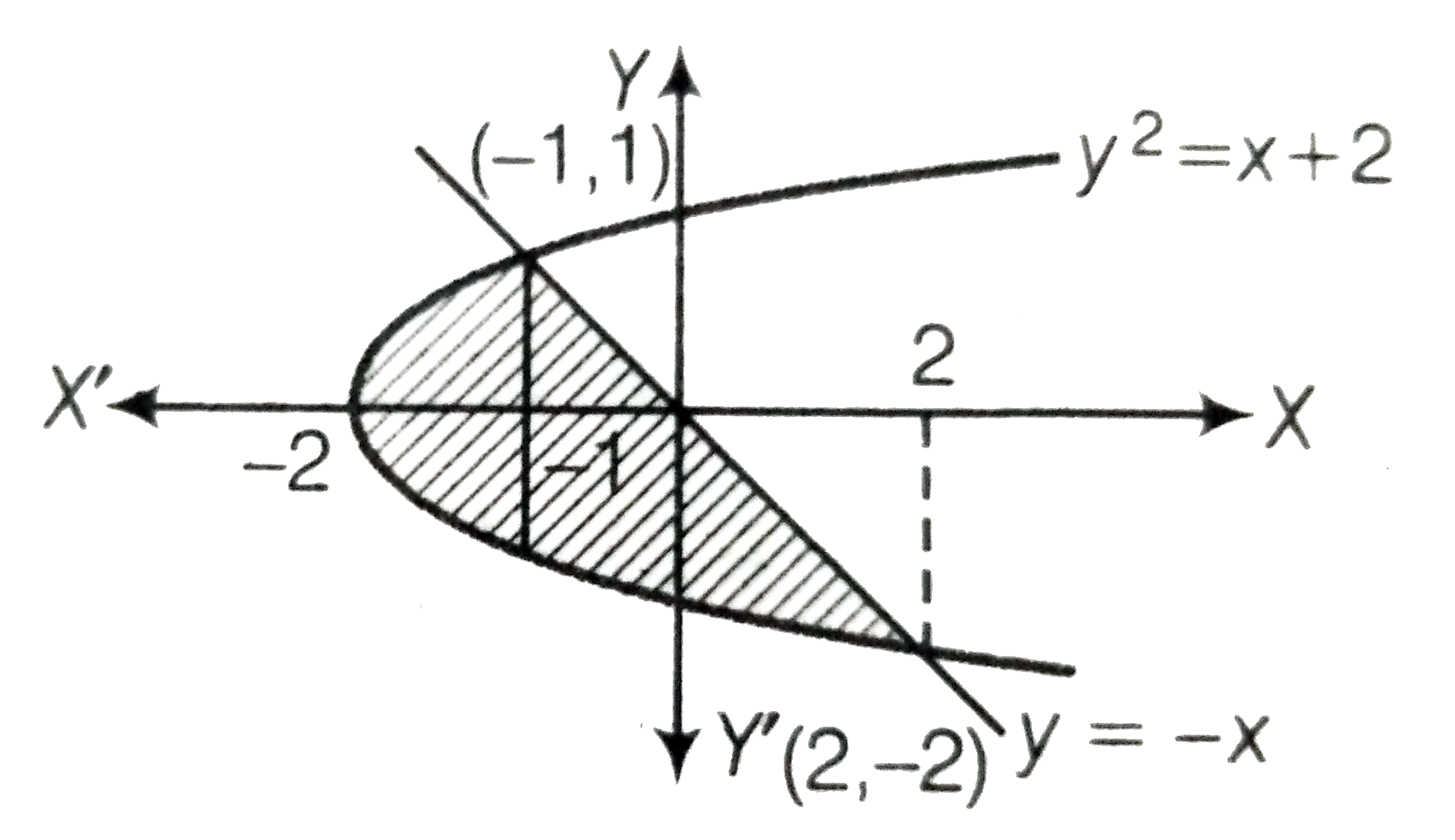
Now, Required area
$= 2 - 1 \int - 2 \sqrt{x + 2} d x + 2 \int - 1 (- x + \sqrt{x + 2}) d x$
$= \frac{4}{3} {[{(x + 2)}^{3 / 2}]}_{- 2}^{3 / 2} + {[\frac{- x^{2}}{2} + \frac{2}{3} {(x + 2)}^{3 / 2}]}_{- 1}^{3 / 2}$
$\frac{4}{3} {(1)}^{3 / 2} + [\frac{- {(2)}^{2}}{2} + \frac{2}{3} {(4)}^{3 / 2}] - [- \frac{{(- 1)}^{2}}{2} + \frac{2}{3} {(1)}^{3 / 2}]$
$\frac{4}{3} - 2 + \frac{2}{3} .8 + \frac{1}{2} - \frac{2}{3} = \frac{4 + 16 - 2}{3} - 2 + \frac{1}{2} = 6 - \frac{3}{2} = \frac{9}{2}$

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area of the region bounded by the curve $y = x^{2}$ and the line $y = 16$ is :
A $\frac{32}{3}$
B $\frac{256}{3}$
C $\frac{64}{3}$
D $\frac{128}{3}$
The area of the region bounded by the curves $x = y^{2} - 2$ and x=y is
A $\frac{9}{4}$
B9
C $\frac{9}{2}$
D $\frac{9}{7}$
The area of the region bouned by the curve $y = 2 x - x^{2}$ and the line $y = x$ is
A $1 / 2$
B $1 / 3$
C $1 / 4$
D $1 / 6$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DEFINITE INTEGRALS -Exercise 2

Home
Ask Doubt
Profile